Chapter 6
マクスウェルの方程式の意味
長い道のりの末ようやくマクスウェルの方程式が全て揃いました。
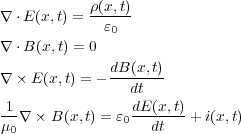
6.1 ガウスの法則と発散のイメージ
さてガウスの法則と磁場に関するガウスの法則
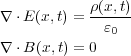
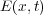 、磁場
、磁場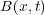 に
に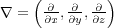 をかけたものです。これは電場
をかけたものです。これは電場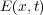 、磁場
、磁場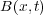 の
「発散」といいます。しかしこれがなんで「発散」なんだ?と感じるかもしれません。数学的には1章でやった「ガウスの
定理」式(2.10)によるんですが、ここでは数学的厳密性は置いといてもう少し感覚的にこの「発散」について考えてみま
す。
の
「発散」といいます。しかしこれがなんで「発散」なんだ?と感じるかもしれません。数学的には1章でやった「ガウスの
定理」式(2.10)によるんですが、ここでは数学的厳密性は置いといてもう少し感覚的にこの「発散」について考えてみま
す。
まず、簡単のため1次元で考えます。ある量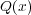 があって、これが
があって、これが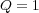 だけあるとベクトル量
だけあるとベクトル量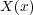 を量 1 だけ
放出(発散)するものとします。つまり
を量 1 だけ
放出(発散)するものとします。つまり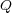 は発生源のようなもので、
は発生源のようなもので、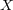 がその出ていくもので、ライトと光あるいは蛇
口と水の流れ、または電荷と電場のような関係です。
がその出ていくもので、ライトと光あるいは蛇
口と水の流れ、または電荷と電場のような関係です。
さてこの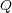 の長さに対しての密度、線密度が
の長さに対しての密度、線密度が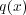 であるとし、図のようにある短い長さ
であるとし、図のようにある短い長さ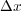 だけ
だけ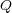 があるときそ
こから放出される
があるときそ
こから放出される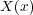 の量は当然その
の量は当然その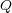 の量で
の量で
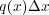
ですが、ここで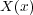 を調べて
を調べて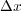 から出ていく量を求めると
から出ていく量を求めると
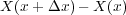
ですね。よって
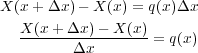
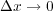 とすればまさに微分で
とすればまさに微分で
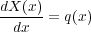
これが3次元なら、もう2方向ぶん足し合わせ、線密度は体積密度にすればいいので
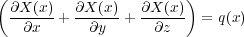
となり、これはまさに
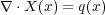
で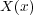 の発散となりました。
の発散となりました。
さて、これでどうして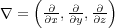 をかけたものが「発散」なのかなんとなくわかってもらえたかと思いいま
す。そこであらためてガウスの法則と磁場に関するガウスの法則を見てみると
をかけたものが「発散」なのかなんとなくわかってもらえたかと思いいま
す。そこであらためてガウスの法則と磁場に関するガウスの法則を見てみると
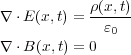
 だけでていくことを意味していて、磁場に関するガウスの
法則では磁場は「発散」していかない、ということを表していることが式からイメージできるかと思いま
す。
だけでていくことを意味していて、磁場に関するガウスの
法則では磁場は「発散」していかない、ということを表していることが式からイメージできるかと思いま
す。
電場に関してはなんだか当たり前のことを意味しているんだなという印象ですが、磁場に関しては「発散」していかな いというのが変な感じですよね。これだとまるで磁場ができないように感じるかもしれませんがもちろんそうではありませ ん。磁場を水の流れに例えるなら、今存在しないといっているのは蛇口、または排水溝です。決して水自体がないとは言っ ていません。蛇口と排水溝を使わずにプールに溜まった水に流れを作るには、小学校の水泳の時間にやったようにプール の中を「回転する」流れにしてやればいいんです。つまり、「磁場には始点や終点はなくすべてループに なっている」というのが磁場に関するガウスの法則が示すものなのです。これで、この二つの法則について イメージできたかと思います。ややこしい数学で導いた式ですが意味しているのは単純なイメージなんで す。
6.2 回転のイメージ
さて残りのマクスウェルの方程式2つは
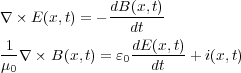
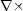 という
という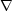 の外積ですね。これは別名
「回転(rotation)」というくらいなので、回転を表しているんですが、なぜこれが回転なの?と感じることでしょう。も
ちろん数学的には3章の「ストークスの定理」式(4.2)からということなんですがそれじゃあわかりずらいので、また感
覚的に見ていきたいと思います。
の外積ですね。これは別名
「回転(rotation)」というくらいなので、回転を表しているんですが、なぜこれが回転なの?と感じることでしょう。も
ちろん数学的には3章の「ストークスの定理」式(4.2)からということなんですがそれじゃあわかりずらいので、また感
覚的に見ていきたいと思います。
この「回転(rotation)」のイメージは直径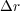 の小さな水車のような感じです。水車が回ると右ねじの進む方向にそ
の水車に仕掛けられたものを押し出すようにできています、またその逆にも動きます。まあ、とりあえず
の小さな水車のような感じです。水車が回ると右ねじの進む方向にそ
の水車に仕掛けられたものを押し出すようにできています、またその逆にも動きます。まあ、とりあえず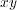 平面にこの水
車を置いてみましょう。水の流れは
平面にこの水
車を置いてみましょう。水の流れは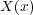 で表します。
で表します。
さて、この水車を図の方向に回すためには水車の右で下(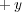 )方向、あるいは左で上(
)方向、あるいは左で上(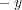 )方向の流れがあ
ればいいですね。左右に水流があるならその水流に差があれば水車はゆっくりですが回りますよね。つま
り
)方向の流れがあ
ればいいですね。左右に水流があるならその水流に差があれば水車はゆっくりですが回りますよね。つま
り
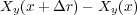
が正ならば回るわけです。また水車の上で右( )方向、あるいは下で左(
)方向、あるいは下で左(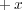 )方向の流れがあっても図の方向に
回るので
)方向の流れがあっても図の方向に
回るので
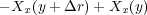
も水車を回転させます。よって
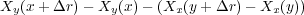
が水車を回転させる力です。水車が回るのはトルクですからこれを直径で割ったものが水車が押し出すものの量です。押し
出すものを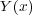 とすると
とすると
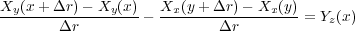
であり、これで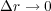 とすれば
とすれば

となり、これはまさに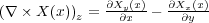 です。
です。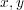 成分についても同様です。これでなんとなくなぜ
「回転」が回転なのかのイメージが掴めてもらえたかと思います。
成分についても同様です。これでなんとなくなぜ
「回転」が回転なのかのイメージが掴めてもらえたかと思います。
さて、改めてあの2式を見てみましょう。まず、ファラデーの法則ですが
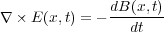
これはつまり単純に磁場が変化するとその周りにぐるっと電場が出来る、ということです。そしてマクスウェル・アンペー ルの法則は
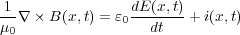
電流と変化する電場の周りに磁場が出来るということを表しているわけです。こうやってイメージでマクスウェルの方程式 を捉えてみると、単純でわかりやすい式であることがわかってもらえたでしょうか?


