Chapter 5
アンペール・マクスウェルの法則
5.1 マクスウェルの方程式、最後の式
さて、ここまでに
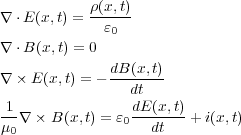
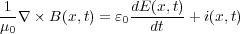
ですが、これは式(3.14)のアンペールの法則
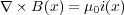
にそっくりですね。これを時間も含む形に一般化してやって、あとは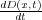 をくっつけてやればそのものですね。そ
の
をくっつけてやればそのものですね。そ
の
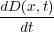
の項は「マクスウェルの変位電流」と呼ばれるものです。実は、ガウスの法則やファラデーの電磁誘導の法則をまと めた四つの式が「マクスウェルの方程式」と呼ばれているのは、マクスウェルがこの項を見つけて、整理 したからなのです。なんだかずるい気もしますが、逆に言うとこの項がそれだけすごい発見だったわけで す。
さて、この項をいかにして導入するかについてはまず、アンペールの法則が時間を含む形に一般化できな かったわけを思い出しましょう。それはアンペールの法則を導くのに時間を含まない「定常電流の保存則」 (3.2)
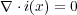
を使っていたからでした。ので、まずは時間を含む電流を記述する式を何か考えなくてはいけません。
5.2 電荷保存則
定常電流でない時間を含む電流は保存されませんが、高校で習うように電荷の総量は保存されます。これは質量保存則のよ うに突然電荷がきえたり現れたりしないという至極当たり前の法則です。
これから、時間を含む電流に関する式を導きたいと思います。いま、適当な空間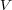 を考えその
を考えその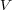 を囲む閉曲面
を囲む閉曲面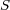 を
通って単位時間当たりに
を
通って単位時間当たりに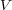 から流れでる電荷の量は、電流の面積分
から流れでる電荷の量は、電流の面積分
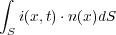
と書ける。また、空間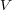 の電荷密度
の電荷密度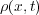 に関して考えると、
に関して考えると、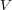 の全電荷の減少量は
の全電荷の減少量は
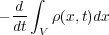
とかけ、この二つが電荷保存則より等しいので
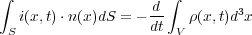
これを微分形に書き直すには、左辺にガウスの法則を使って
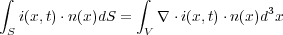
また、右辺の時間微分を積分の中にいれると
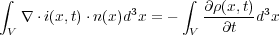
これを微分し
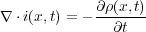 | (5.1) |
これが微分形で表した「電荷保存則」です。
5.3 マクスウェルの変位電流
さて、もう一度式(3.14)のアンペールの法則を見てみましょう。
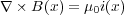
これは時間 を含む形には何度も言うように拡張できないんですが、ためしに無理やりやってみると
を含む形には何度も言うように拡張できないんですが、ためしに無理やりやってみると
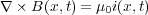
しかし、これの発散を取ると
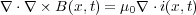
ベクトル解析の公式で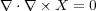 から
から
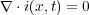
となり、これは明らかに電荷保存則(5.1)
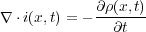
と矛盾してしまいます。
じゃあ、要するにこの電荷保存則を満たすようにアンペールの法則を拡張してやろうと思った(であろう)のがマクス ウェルです。アンペールの法則を例のマクスウェルの変位電流の項を加えたものは
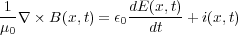
ですが、さてこれの発散を同じように取ると
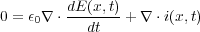
ここでガウスの法則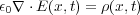 を使うと
を使うと
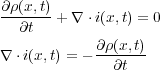
よってこれでアンペールの法則が時間に関して一般化でき、この式
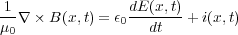 | (5.2) |
を「アンペール・マクスウェルの法則」といいます。これでようやくマクスウェルの方程式最後の式が得られまし た。
