Chapter 4
電磁誘導
4.1 ファラデーの電磁誘導の法則
前章では電流が流れると磁場が出来るということをやってきたのですが、ファラデーという人はこれの逆も成り立つんじゃ ないかと考え、コイルに囲まれた部分の磁場の量(磁束)が変化するとコイルに電流が流れることを発見しました。これを 電磁誘導といいます。
さて、この現象を式にすると、電流が生じるというのはつまりコイルに起電力(電圧)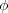 がかかっているということな
ので、これが磁束
がかかっているということな
ので、これが磁束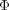 の変化に比例しているので
の変化に比例しているので
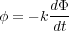 | (4.1) |
となります。ここで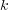 は比例定数ですが、起電力(電圧)
は比例定数ですが、起電力(電圧)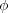 の単位をボルト、磁束
の単位をボルト、磁束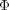 の単位をウェー
バーとすると
の単位をウェー
バーとすると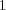 になります。というより1になるように単位を決めたいうのが正しいですが。また右辺
の負号は、磁束の変化を打ち消すような磁場が出来る向きに電流が生じることをわかりやすくするためで
す。
になります。というより1になるように単位を決めたいうのが正しいですが。また右辺
の負号は、磁束の変化を打ち消すような磁場が出来る向きに電流が生じることをわかりやすくするためで
す。
さて、ここで起電力とはコイルを一周したとき単位電荷の粒子が得るエネルギーなので
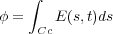
と書け、磁束のほうは、コイルに囲まれた部分全体の磁場の量なので
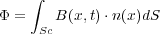
これから
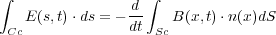
と書けるが、さてここで積分範囲の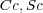 はそれぞれコイルの周とその囲まれた面積だったわけですが、ファラデーはこ
こで発想の大きな飛躍をします。というのは、ファラデーはこのコイルのあるなしに関われず、磁束の変化した空間に電場
が発生するのだと考えたのです。そしてたまたまその発生した電場のあるところにコイルがあれば電流が流れる、と。そう
考えると積分範囲は任意の
はそれぞれコイルの周とその囲まれた面積だったわけですが、ファラデーはこ
こで発想の大きな飛躍をします。というのは、ファラデーはこのコイルのあるなしに関われず、磁束の変化した空間に電場
が発生するのだと考えたのです。そしてたまたまその発生した電場のあるところにコイルがあれば電流が流れる、と。そう
考えると積分範囲は任意の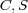 となり
となり
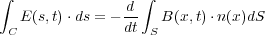
例によって例のごとくこの式を微分形にしたいのですが、ガウスの定理は使えない形なので、新しい定理を使いま す。
4.2 ストークスの定理
その新しい定理というのがストークスの定理なのですが、これは任意のベクトル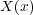 に対して
に対して
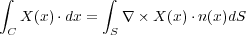 | (4.2) |
という関係が成り立つことです。ここで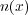 は面
は面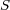 の点
の点 における単位法線ベクトルです。このストークスの定理は
における単位法線ベクトルです。このストークスの定理は
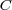 上の線積分を面
上の線積分を面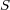 に対する面積分に書き換える公式で電磁気でガウスの定理と共に最も使われる定理ですので是非覚え
ておいてください。
に対する面積分に書き換える公式で電磁気でガウスの定理と共に最も使われる定理ですので是非覚え
ておいてください。
さてこの証明ですが、少々面倒なので厳密にではなく感覚的にやりたいと思います。厳密な証明が知りたい人は他の電 磁気の本を広げてください。
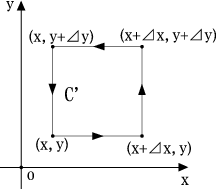
まず、簡単のため考える平面を図のように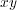 平面上の微小な四角形とします。そして図の矢印の向きに
平面上の微小な四角形とします。そして図の矢印の向きに に沿って
線積分すると
に沿って
線積分すると
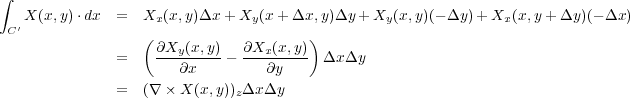
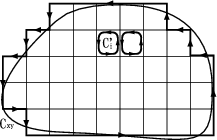
ここでまたガウスの定理と同じような感じに、任意の平面は図のように微小な四角形の足し合わせと書けるの で、
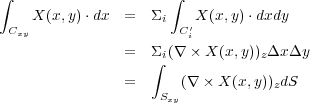
 平面上では
平面上では
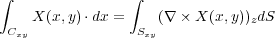
が言えた。当然同様にして 平面上で
平面上で
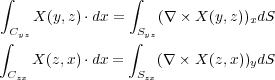
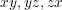 平面にまたがっているので、それぞれの足し合わせ
で
平面にまたがっているので、それぞれの足し合わせ
で
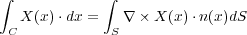
となりストークスの定理が証明できました。
4.3 微分形のファラデーの法則
さて、このストークスの定理を使って
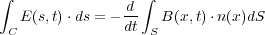
を微分形に直します。左辺にストークスの定理を使い、右辺の時間微分を積分の中に入れると
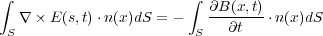
よってこれを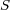 で微分し
で微分し
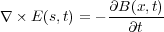 | (4.3) |
となります。これを「微分形のファラデーの法則」といいマクスウェルの方程式の三つ目です。