Chapter 7
電磁波
7.1 電磁波の波動方程式
さて、マクスウェル方程式の応用として電磁波を考えて見ましょう。まず、電流、電荷が共にない空間(自由空間といいま す)を考えるとマクスウェル方程式は
となりますね。ここでちょっと式(7.3)、(7.4)を見てみましょう。式(7.2)からわかるように電場 E が時間変化する ときその周りに磁場 B ができます。また式(7.3)からその出来た磁場 B からまた電場 E’が出来ます。これが無限に繰り 返されるのでどんどん遠くまで電場磁場が到達します。 これがつまり電磁波です。もし式(7.4)のマクスウェルの変位電流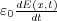 がなかったら当然この連
鎖は続きません。マクスウェルの偉大さはなんといってもこの項をいれ、そして電磁波を予想したことで
しょう。さて、ではこの電磁波をちゃんと数学で書いてみましょう。式(7.4)に左から
がなかったら当然この連
鎖は続きません。マクスウェルの偉大さはなんといってもこの項をいれ、そして電磁波を予想したことで
しょう。さて、ではこの電磁波をちゃんと数学で書いてみましょう。式(7.4)に左から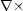 をかけてやる
と
をかけてやる
と
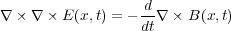
ここでベクトル解析の公式(3.12)より
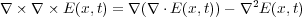
また、式(7.1)より
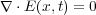
なので、結局
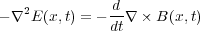
一方式(7.4)より
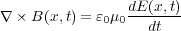
なので最終的に
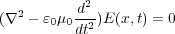 | (7.5) |
という式が得られます。実はこの式は波動方程式という一般に波を表す式の形なのです。磁場についても式(7.4)から同 じようにして
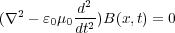 | (7.6) |
が得られます。さてこれらが実際に波を表しているか見てみましょう。
7.2 波動方程式の解
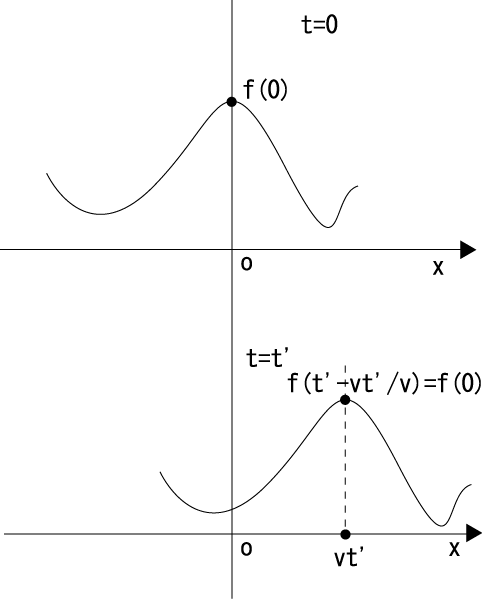
波動方程式の解というと、例えば
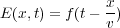
と言うものがあります。これは図のように適当な関数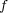 が時間t進むとvだけx方向に進んでいく「波」のことを意味し
ています。
が時間t進むとvだけx方向に進んでいく「波」のことを意味し
ています。
さて、これを試しに式(7.5)代入してみましょう。
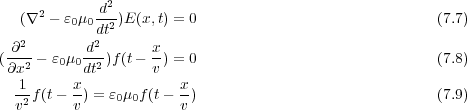
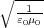 であることがわかります。じつはこの値
であることがわかります。じつはこの値![sqrt-1--= 3× 108[m ∕s2]
ε0μ0](elct337x.png) は実
験で測られた光の速度と非常によく一致します。これはつまりどういうことかといえば、「光は電磁波、電磁波は光」だっ
たというわけなのです。
は実
験で測られた光の速度と非常によく一致します。これはつまりどういうことかといえば、「光は電磁波、電磁波は光」だっ
たというわけなのです。
7.3 マクスウェル方程式の問題と相対論
前章で光速が![3 ×108[m∕s2]](elct338x.png) と求まったわけですが実はこれにはある問題が隠れています。聡明な人なら気づいたかもし
れませんがその問題とは
と求まったわけですが実はこれにはある問題が隠れています。聡明な人なら気づいたかもし
れませんがその問題とは
「この光の速度は何に対しての速度なのか?」
というものです。電磁波というくらいですからまず一般の波の場合を考えてみましょう。さて普通波の速度とは媒質に 対しての速度です。例えば空気中の音波なら空気からみてどれくらいの速度かいうのが音速です。海の波なら海面に対して です。船かなんかで海面を突っ切れば波を追い越したりできますよね。では電磁波、光の場合はどうでしょう?媒質は といえば…特に思いつきませんね。電磁波は電場、磁場が交互にできるものですから媒質というとこの電 場、磁場の媒質ですがそんなものは特に考えてきませんでした。そこで昔の人はこの媒質に「エーテル」と いう名前をつけ光速はこれに対しての速度だと考えました。さて、そうなればこのエーテルを探そうとさ まざまな人たちががんばりました。そこで地球も宇宙空間、すなわちエーテル内を移動しているわけだか ら、それによって光速度に違いがでるだろうと高精度の実験(「マイケルソン・モーレーの実験」)を行い ましたが、その結果は意外にも「光速度に違いはない」というものだったのです。さてこの結果をどう考 えるべきかいらいろな人がいろいろなことを考えましたがここでかのアインシュタインは、実にシンプル に
「光速度に違いはないのはつまりエーテルは存在しない。光速度は何に対しても同じなのだ」
と考えたのです。この前提(光速度不変)からあの有名な相対論が作られました。
相対論についてもいずれ書きたいと思います。