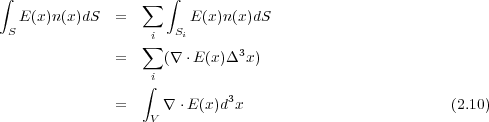Chapter 2
クーロンの法則とガウスの定理
2.1 クーロンの法則と電場
というわけで、さっそくマクスウェル方程式の一つ目、
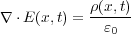
を導いていきましょう。実はこの式、高校やもしかすると中学でやったクーロンの法則なんです。「全然違うだろ!!」と 思うかもしれませんが、クーロンの法則をガウスの定理を使って書き直すとこうなるんです。それを順を追ってみていきま す。
それにはまず復習から行きましょう。電磁気学の歴史としては、この式
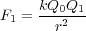 | (2.1) |
クーロンの法則から出発します。これは点電荷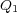 に働く力の大きさ
に働く力の大きさ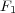 が点電荷
が点電荷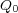 ,
,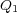 に比例して、距離rの2乗
に比例して、距離rの2乗
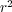 に反比例するという実験事実を式にしたものです。
に反比例するという実験事実を式にしたものです。
このままでは、中高レベルですので、大学らしくこの式をベクトルで書き直してみましょう。
すると
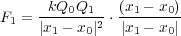 | (2.2) |
となります。右辺第二項が点電荷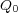 から
から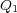 へのベクトル(向き)を示しています。絶対値で割ってあるのは大きさを
1にするためです。さて、ところでこの力は「いつから」働くんでしょうか?
へのベクトル(向き)を示しています。絶対値で割ってあるのは大きさを
1にするためです。さて、ところでこの力は「いつから」働くんでしょうか?
もし片方の電荷がぽんっと突然現れたとすると、もう一方はいつから力を感じるでしょうか?その瞬間からでしょうか?宇
宙の端と端とでも?
それはちょっと考えにくいので、電荷はまず「電場」を自分の周りに作り、この電場がほかの電荷に力を及ぼすと考えてみ
ましょう。電場の強さ = 働く力 / 力を感じる電荷、として先ほどのクーロンの法則を電場というものを考えて書き直す
と

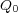 が空間に電場
が空間に電場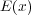 を作り、それが
を作り、それが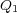 に力を及ぼしていることを式にしたもので
す。
に力を及ぼしていることを式にしたもので
す。 さて、「で、結局電場ってなんだよ?よくわからんもん勝手につくるなよ!」とか思った人もいるのではないでしょう
か?
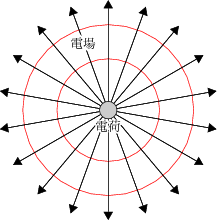
電場とは結局最初はこのように「なんとな〜くあるんじゃないかな〜」とファラデーが考えだしたものです。実際、昔はそ
んな不確かな電場の存在を頑なに認めない人も結構いたそうです。ただ教科書の絵のように電荷からたくさんの矢印が出て
いる図は直感的にわかりやすいですよね。電場なんかなく「電荷から電荷に何も介さずに力が働く」という考え方を「遠隔
作用」と呼び、電場なんかが介しているんだという考えを「近接作用」をいいます。しばらくこの「遠隔 v.s 近接」の論争
は平行線をたどるのですが近接作用、つまり電場磁場の考えはマクスウェルにより美しくまとめられ、さらに「電磁波」の
存在を予言しました。ご存知のようにこの電磁波が予言どおり発見され「遠隔 v.s 近接」の論争にピリオ
ドが打たれたのです。そんなわけなんでとりあえず電場の存在を認めてもらって話をすすめていきましょ
う。
普通、電荷が点電荷とは限らないので、電荷が体積 V の大きさを持っているときは、電荷密度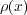 を
を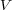 で積分して
やったもの
で積分して
やったもの
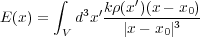 | (2.5) |
で表せます。この式を計算できればあらゆる形の電荷の作る電場を求めることができます。その例を以下で見てみましょ う。
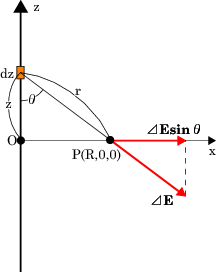
例題無限に長い直線状の電荷の電場
さて、上の式を使えば様々な形状の電荷の作る電場を求めることが理論的にはできますが、実際は積分計算なので厳密に解
けるのは限られた場合だけです。例えば、電荷の線密度が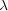 であるような無限に長い直線状の電荷の作る電場を考えてみ
ましょう。電荷は z 軸に沿ってあるとします。ここで
であるような無限に長い直線状の電荷の作る電場を考えてみ
ましょう。電荷は z 軸に沿ってあるとします。ここで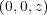 にある電荷の微小部分
にある電荷の微小部分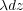 は点電荷とみなせるので、それ
が点
は点電荷とみなせるので、それ
が点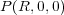 に作る電場の強さは、
に作る電場の強さは、
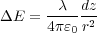
しかし、電荷の直線は無限に長いので、直線に直交する成分以外は相殺されます。ので残る直交の成分は
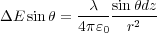
さて、図より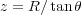 よって
よって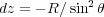 、また
、また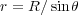 なのでこれらを代入する
と
なのでこれらを代入する
と
2.2 ガウスの法則
とりあえず、クーロンの法則(2.5)
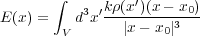
を使えば積分できればあらゆる形の電荷からできる電場を求めることができる、ということがわかりまし
た。
ということはこれこそが基礎方程式のひとつであるべきじゃないか?と思うかもしれません。そうなんです、これが基本式
のひとつです。
ただちょっと書き直すとさっきの
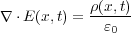
になります。
「なんでわざわざ書き直すんだ?!同じならわざわざわけわからない式にしなくていいじゃないか!」
と思うかもしれません。書き直す前のは「電荷があると電場はどうできるか?」という式の形をしています。つまり電荷が
主語なのです。しかしさっき僕らは電場の存在を認めたんでした。なら電場を主役にして書き直してみようじゃないか!っ
てのが書き直す動機です。今後この「場」の考え方は様々なところに応用され成功します。そんなわけなんでなんとか納得
してもらって話をすすめましょう。
さて電場に関しての式を書くにしたがって、最低限の条件をまとめてみましょう
- 電場とは電荷の量に比例してから生まれる(消える)矢のようなイメージ
- 電荷が関係しなければ勝手に増えたり消えたりしない
- 一方向に偏ることなく満遍なく広がる(空間に対して対称性がある、といいます)
さて、次に目指すのはこのことを数式にして法則化することです。物理ってのは「物事を数式にすること」といえるでしょ
う。
そのために次のようなイメージを考えてみてください。
あるところに電荷があり、それを風呂敷かなんかでぐるっと囲みます。するとその風呂敷を突き抜けていく(- なら入って
くる)電場の矢の総数は当然中でできた電場の量、つまり電荷に比例しますね。これは風呂敷にスキマがなければよくて別
に大きさや包み方には拠りません。
こんなイメージをさっそく式にしてみましょう。まず風呂敷、というとあれなのでぐるっと閉じた面という意味で以下
「閉曲面」といいます。でその閉曲面の一部を拡大してみてみます。充分小さな面積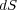 をとってくればそこは平らで電場
の向きと大きさは同じと考えていいでしょう。そこの電場
をとってくればそこは平らで電場
の向きと大きさは同じと考えていいでしょう。そこの電場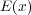 がその面をどれだけ貫いていくかはその電場の向きにより
ます。もし面に垂直なら 100 %貫いていくし、反対に水平なら全然出て行ってないですね。つまりその電場の
面に垂直な成分だけが貫くわけです。そこで面に垂直な大きさ1のベクトル(単位法線ベクトルといいま
す)
がその面をどれだけ貫いていくかはその電場の向きにより
ます。もし面に垂直なら 100 %貫いていくし、反対に水平なら全然出て行ってないですね。つまりその電場の
面に垂直な成分だけが貫くわけです。そこで面に垂直な大きさ1のベクトル(単位法線ベクトルといいま
す)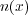 と電場
と電場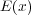 との内積をとってやればそれが出て行く(- なら入ってくる)電場の量になりま
す。
との内積をとってやればそれが出て行く(- なら入ってくる)電場の量になりま
す。
さて、この量を閉曲面の全部分で計算し足し合わせたもの
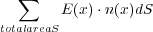
が閉曲面を出て行く(入ってくる)電場の総量すなわち中の電荷の量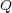 と比例するわけです。
と比例するわけです。
ところで微小部分を計算し足し合わせるってのは要するに積分するってことですよね。なので比例係数を とトキトーに
とってまとめて書き直すと
とトキトーに
とってまとめて書き直すと
 が割ってあるのはガウスさんが最初に比例係数
が割ってあるのはガウスさんが最初に比例係数
 を電場側にかけるように決めたんですが電場側にかかってると不便だったので割っただけにすぎませ
ん。さてこれで一応数式になったんですが「なんか余計にわかりにくくなったぞ」と思っている人もいる
かもしれません。でも、この式なかなかすごいんですよ、なにがすごいかちょっと具体的に見てみましょ
う。
を電場側にかけるように決めたんですが電場側にかかってると不便だったので割っただけにすぎませ
ん。さてこれで一応数式になったんですが「なんか余計にわかりにくくなったぞ」と思っている人もいる
かもしれません。でも、この式なかなかすごいんですよ、なにがすごいかちょっと具体的に見てみましょ
う。
例題点電荷の作る電場
基本にもどり、点電荷 Q の場合にガウスの法則を当てはめて見ましょう、まず次の図のように点電荷を中心にぐるっと半径
 の球で囲んでみましょう。
の球で囲んでみましょう。
今点電荷は球の中心にいるので、放射上に広がる電場と球面と垂直、しかも大きさは球面のどこでも一緒なのでガウス の法則は
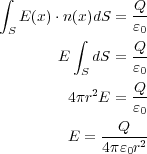
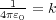 と書き直してやると、これはまさにクーロンの法則ですね。これでちゃんとクーロンの法則=ガウスの法
則がわかりました。
と書き直してやると、これはまさにクーロンの法則ですね。これでちゃんとクーロンの法則=ガウスの法
則がわかりました。「おんなじならやっぱりクーロンの法則のままでいいじゃんか!結局ガウスのどこがすごいんだよ?!」
という突っ込みの答えは、ずばり「r の逆二乗」です!
なぜ E が r の逆二乗に比例することはクーロンの法則では「実験事実である」という説明しかできません。もしかしたら きっちり2じゃなくて 2.0013 かもという可能性すら残ってます。ところがガウスの法則では式を追ってみると「ほら、球 の表面積からでてくるよ」と r の逆二乗を説明できるわけです!そんなわけで一歩リードしているガウスの法則が基本法則 になったわけです。
例題無限に長い直線状の電荷の電場
つづいて、この積分形のガウスの法則を使って、先ほどクーロンの法則で求めた問題を解いてみよう。直線を中心とする厚
さが 1 で半径が の円筒を考え、その表面で積分形のガウスの法則を使います。今、電場は半径方向にあるの
で、円筒のフタの部分は寄与しません。側面の単位法線ベクトル
の円筒を考え、その表面で積分形のガウスの法則を使います。今、電場は半径方向にあるの
で、円筒のフタの部分は寄与しません。側面の単位法線ベクトル は電場と平行なのでそのままかけられ
て、
は電場と平行なのでそのままかけられ
て、
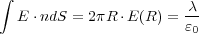
よって
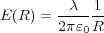
と先ほどのクーロンの法則から求めるのよりも大分簡単に式(2.6)が得られることがわかりますね。
2.3 微分系のガウスの法則
さて、無事電場に関する式である積分形のガウスの法則(2.7)
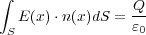
を導けてめでたしめでたしといきたいところですが、この章の目標であったあの式
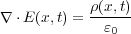
がまだ出てきません。この式の名前は「微分系のガウスの法則」といい、積分形のガウスの法則とは親戚、いや同じ人物の
右側と左側のようなものです。
実際、積分系のガウスの法則の Q は閉曲面内の電荷という意味だったので電荷密度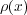 を使って書き直す
と
を使って書き直す
と
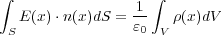 | (2.8) |
となり大分似ていることがわかると思います。ただ問題は左辺は面積 S の積分(2次元)、右辺は体積 V の積分(3次
元)なので単純に微分できないことです。その辺の問題を解決するためにあの変な三角形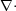 とか出てくるわけで
す。
とか出てくるわけで
す。
「積分系のガウスの法則で電場がもとまるならそれでいいじゃないか!なぜわざわざ微分形に書き直すのか?」というと、
積分系は当然「電場の集まりの性質」を記述したものです。そりゃそうでしよね、足し上げてるんですから。今目指すは
「電場」の性質を記述する式なわけです。そのためには積分しない式の形、つまりは微分系にしたいわけで
す。
2.3.1 ガウスの定理
さっそく微分形に書き直すに当たって、まずガウスの定理というものを証明します。もうちょっと簡単な説明がいい人
は6章「マクスウェルの方程式の意味」を参照してください。
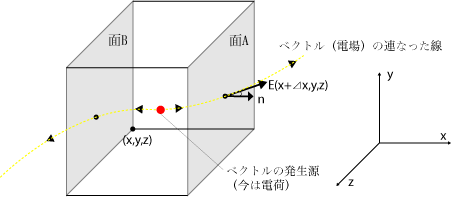
さて、体積が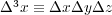 な微小な箱を考えて、その近辺の電場(電場じゃなくても任意のベクトルでこの定理は成
り立ちます)を表面積
な微小な箱を考えて、その近辺の電場(電場じゃなくても任意のベクトルでこの定理は成
り立ちます)を表面積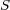 で面積分することを考えます。
で面積分することを考えます。
まず、 x 軸に垂直な二面 A、 B について考えます。 A を貫く電場の強さは 方向の電場なので
方向の電場なので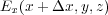 、
A の面積は
、
A の面積は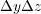 なので
なので
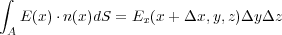
B では、貫く電場の向きが 方向のマイナスなことを考慮するとあとは一緒で
方向のマイナスなことを考慮するとあとは一緒で
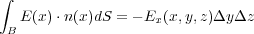
この二つを合わせて
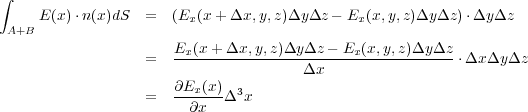
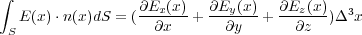
ここで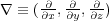 というものを考えると上の式は
というものを考えると上の式は
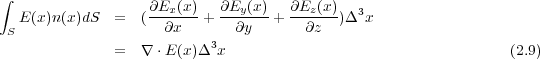
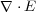 を
を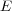 の「発散」(divergence)と言います。その理由はこれがこのベクトル、今は電場が微小
な箱から (単位時間に) 出て行く量を表しているからです。本によっては、この
の「発散」(divergence)と言います。その理由はこれがこのベクトル、今は電場が微小
な箱から (単位時間に) 出て行く量を表しているからです。本によっては、この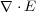 を「発散」と言う意味で
を「発散」と言う意味で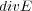 と書
くものをあります。
と書
くものをあります。
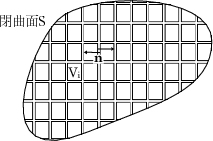
ところで、今任意の閉曲面のとき、図のようにたくさんの微小な箱に分割し
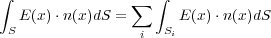
と書けます。これは の隣り合う面同士は
の隣り合う面同士は が逆向きなので相殺され、結局隣り合う面のない面だけが足し合わされ
る、つまり閉曲面
が逆向きなので相殺され、結局隣り合う面のない面だけが足し合わされ
る、つまり閉曲面 だけになるからです。よって
だけになるからです。よって
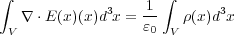
となります。これを両辺微分すれば、
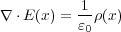
となり、今までの議論は電場・電荷密度が時間を含む関数であっても問題ないので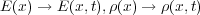 とす
ると、やっと目的だった微分形のガウスの法則
とす
ると、やっと目的だった微分形のガウスの法則
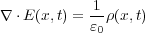 | (2.11) |
となります。この式はつまり微小な箱から出てくる電場の量はその箱の電荷の量に比例し、電荷がないときは電場はない か、または箱を素通りしていく、というごく当たり前なことを表しているわけです。ただ、微分形の数式にすることで解析 的に扱え、例えば電磁波などを導けるのです。