Chapter 3
磁場
3.1 アンペールの力
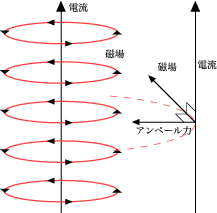
電場の基本法則が導けたので次は磁場です。磁場というと、よくあるあの磁石から出ている線で表されるもののことです が、ここでは磁石ではなく電流から生じる磁場について考えていきます。
磁場があるとどうなるのかをとりあえず知らないと磁場がどうなっているのか知れてもうれしくありません。のでここ からはまず、磁場からはどんな力を受けるのかについて述べていきます。内容的には高校までにやるものと同じなので、わ かっている人は「定常電流」の章以外は読み飛ばしてください。
さて、一本の導線に電流を流し、もう一本電流を流した導線を近づけると力が働きます。これがアンペールの力です。 これは電場と同じように電流の周りにまず、磁場というものができて、その磁場から電流が力を受けると考えま す。
電流からできる磁場は実験から、電流の方向に対して右回りに、円状にできることがわかっています。そし て、力は下図のように働くことがわかっています。これはよくフレミングの左手の法則として知られていま す。
3.1.1 ベクトル積
ずっと左手をこちゃこちゃして力の方向を求めているわけにもいかないので、数学の言葉でフレミングの左手の法則を表し
てやりましょう。そのために、ベクトル積というものを考えます。いま、ベクトル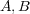 があるとします。そのベクトル積
は
があるとします。そのベクトル積
は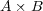 と書き、これは大きさが
と書き、これは大きさが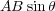 で、方向が
で、方向が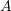 と
と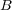 に垂直で
に垂直で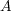 から
から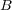 に回して右ねじが進む方向を向い
ているベクトルです。(
に回して右ねじが進む方向を向い
ているベクトルです。(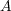 を電流、
を電流、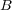 を磁場とすると
を磁場とすると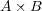 がアンペール力の方向です)つまり、それぞれの単位ベ
クトル
がアンペール力の方向です)つまり、それぞれの単位ベ
クトル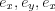 に対して
に対して
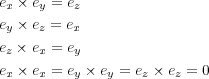
が成り立ちます。これから、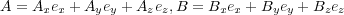 は
は
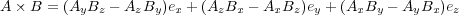
と書けます。これを使い、定常電流 (時間変化しない電流)の導線の微小な部分
(時間変化しない電流)の導線の微小な部分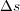 (方向は電流の向き) にかかるアン
ペールの力は
(方向は電流の向き) にかかるアン
ペールの力は
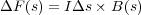 | (3.1) |
と書けます。このように定義した磁場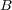 を「磁束密度」といいます。これを導線の形で積分してやれば、導線全体にかか
る力が求まるわけです。
を「磁束密度」といいます。これを導線の形で積分してやれば、導線全体にかか
る力が求まるわけです。
3.2 定常電流
さて、定常電流とは、時間変化しない電流と言いましたがもう少し詳しく説明すると、単位面積当たりの電流の強さを「電
流密度」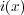 が時間に依存しないとき、その電流を「定常電流」といいます。
が時間に依存しないとき、その電流を「定常電流」といいます。
電流とは単位時間当たりに流れる電荷の量のことでした。定常電流の場合、任意の閉曲面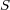 に囲まれた領域
に囲まれた領域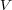 に単位
時間に流れ込む電荷の量は、その領域から出て行く電荷の量と等しくなります(そうでないと流れが淀んでしまいます)。
これを「定常電流の保存則」といいます。この法則を数式にすると、まず、微小面
に単位
時間に流れ込む電荷の量は、その領域から出て行く電荷の量と等しくなります(そうでないと流れが淀んでしまいます)。
これを「定常電流の保存則」といいます。この法則を数式にすると、まず、微小面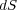 を通過する電荷の量は
を通過する電荷の量は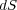 の単位
法線ベクトル
の単位
法線ベクトル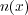 を用いて
を用いて
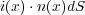
ここで、面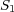 からのみ電荷が入って
からのみ電荷が入って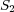 からのみ出て行くような円筒形の領域を適当に取れば、
からのみ出て行くような円筒形の領域を適当に取れば、
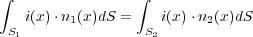
となります。今、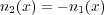 となるので
となるので
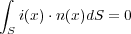
と書け、ガウスの定理(2.10)を使うと
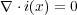 | (3.2) |
となります。
3.3 ローレンツの力
ところで、電流というのは電荷の流れのことなので、上のアンペールの力はすなわち動く電荷に働く力として考えるこ
とができます。それにはまず、導線上の1点 における微小部分をとり、そこにかかるアンペールの力
を考えます。微小部分は断面積
における微小部分をとり、そこにかかるアンペールの力
を考えます。微小部分は断面積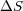 、長さ
、長さ とし、単位体積あたりの力と電流を
とし、単位体積あたりの力と電流を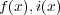 すると力
は
すると力
は
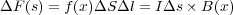
となり、電流は
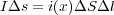
とかけるので
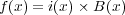
となります。ここで電荷密度を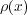 、その速さを
、その速さを とすると、
とすると、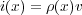 なので
なので
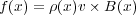 | (3.3) |
電荷 の点電荷の場合には
の点電荷の場合には
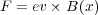 | (3.4) |
となります。
特に点電荷にかかる、電場、磁場からの力をまとめたもの
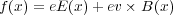 | (3.5) |
をローレンツの力と呼びます。
3.4 ビオ・サバールの法則
さてこれで、磁場があったとき、それによって電流がどう力を受けるかは、わかりましたが、では電流からどのように磁場 ができるのでしょうか?それを求めていくことでマクスウェル方程式の二つ目と四つ目
まず、実験事実として、直線に流れる定常電流の周りにできる磁場は、以下の式で表されます。
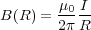 | (3.6) |
つまり、磁場は電流に比例し、電流からの距離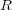 に反比例します。ところでこの式は何かに似ていませんか?一章の例題
の式(2.6)
に反比例します。ところでこの式は何かに似ていませんか?一章の例題
の式(2.6)
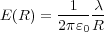
とそっくりですね。式(2.6)がクーロンの法則から導かれてのだから、上の磁場の式から逆にクーロンの 法則と似た式が導けます。これを「ビオ・ザバールの法則」といい、磁束密度の強さは以下の形で書けま す。
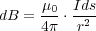
ここで、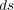 は導線の微小部分です。ところで、電場は放射状に広がっていくの対して、磁場は電流に対して右巻きの渦巻
き状になっています。そのため「ビオ・サバールの法則」をベクトルで書くと
は導線の微小部分です。ところで、電場は放射状に広がっていくの対して、磁場は電流に対して右巻きの渦巻
き状になっています。そのため「ビオ・サバールの法則」をベクトルで書くと
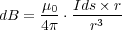 | (3.7) |
となります。
しかし、電流の微小部分、電流素子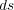 というものは、電流が電荷の流れであることを考えると、電荷と違ってカケラ
単独では存在できず必ず連続してぐるっと一周していないとおかしいですね。また、導線には実際には太さがあるので、そ
れらのことを考慮すると式(3.7)は
というものは、電流が電荷の流れであることを考えると、電荷と違ってカケラ
単独では存在できず必ず連続してぐるっと一周していないとおかしいですね。また、導線には実際には太さがあるので、そ
れらのことを考慮すると式(3.7)は
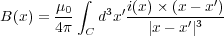 | (3.8) |
となります。ここで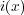 は電流密度です。
は電流密度です。
このビオ・サバールの法則を解けば、基本時にどんな形の電流からできる磁場が求まることになりますが、ただ でさえなかなか解けない積分なのにこんな複雑な形なので、非常に限られたときにしか解けません。そこ で、
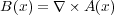 | (3.9) |
という関係のある「ベクトルポテンシャル」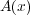 というものを考えてビオ・サバールの法則をもう少し簡単な形に書き換
えます。この
というものを考えてビオ・サバールの法則をもう少し簡単な形に書き換
えます。この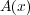 を
を
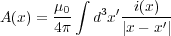 | (3.10) |
と書くと式 (3.9) を満たします。この積分のほうが見た目どおり計算が楽になります。
さて、ちゃんとこの式が式 (3.9) を満たしていることを示します。まず、 成分を計算します。
成分を計算します。
![B (x ) = (∇ × A (x ))
x x
= ∂Az(x)- ∂Ay(x)-
∂y ∫ ∂z ∫
= μ0[ ∂- d3x′ i(x′)z---∂-k d3x′-i(x′)y-]
4π∫∂y |x - x ′| ∂z |x- x′|
μ0- 3 ′ ′ ∂----1--- ′ ∂----1---
= 4π d x[i(x )z ∂y|x- x′| - i(x )y∂z|x- x′|]
μ0∫ i(x′)z(y- y′) i(x′)y(z - z′)
= 4π- d3x′[---|x--x′|3- + --|x--x′|3--]
∫ ′ ′
= μ0- d3x′(i(x)×-(x--x-))x-
4π |x- x′|3](elct151x.png)
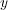 、
、 成分も同様に計算できるので、これでちゃんと満たしていることがわかります。
成分も同様に計算できるので、これでちゃんと満たしていることがわかります。
3.4.1 ベクトル解析の公式
さて、ベクトルポテンシャルとビオ・サバールの法則(3.9)を使って、本題の
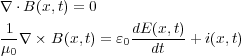
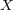 で
で
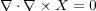 | (3.11) |
が成り立ちます。これは、以下のように簡単な計算です。
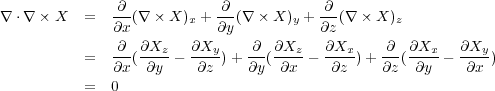
もう一つは
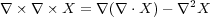 | (3.12) |
ここで、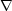 の内積とそうでないものに気をつけてください。内積は前に述べた「発散」ですが、内積でないものは、
の内積とそうでないものに気をつけてください。内積は前に述べた「発散」ですが、内積でないものは、
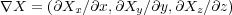 で、「勾配(gradient)」といいます。
で、「勾配(gradient)」といいます。
この証明は 成分を計算し、
成分を計算し、
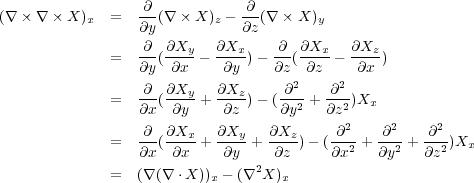
3.5 磁場の基本法則
3.5.1 磁場に関するガウスの法則
さて、ビオ・サバールの法則
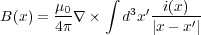
に先ほど求めた式(3.11)を使うと、
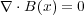
が得られます。これは別に電流密度が時間変化している場合でも成り立って、
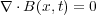 | (3.13) |
と一般化できます。これを「磁場に関するガウスの法則」といいます。これでマクスウェル方程式の二つ目が導けまし た。
3.5.2 微分形のアンペールの法則
さあ、残るもう一つ
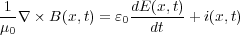
を得るためには、ビオ・サバールの法則に式(3.12)を使い、
![μ0- ∫ 3 ′-i(x)--
∇ × B (x) = 4π∇ × ∇ × d x |x - x′|
μ [ ∫ i(x′) ∫ i(x′) ]
= -0- ∇(∇ ⋅ d3x′-----′)- ∇2 d3x′-----′-
4π |x - x| |x - x|](elct167x.png)
ここで、
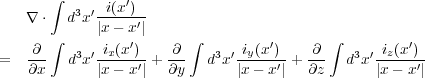
において、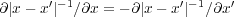 を使い
を使い
![∂ ∫ ix(x′) ∫ ∂ 1
∂x- d3x′|x---x′|- = d3x′ix(x′)∂x-|x---x′|-
∫
= - d3x′ix(x′)-∂′--1--′-
∫ [ ∂x |x -]x|∫
= - d3x′-∂- -ix(x′)- + d3x′---1---∂ix(x′)
∂x′ |x - x ′| |x- x′| ∂x′](elct170x.png)
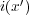 の値が無限大にならないなら、
の値が無限大にならないなら、
![′
∫ 3 ′ ∂ [ ix(x′) ] ∫ ′ ′[ ix(x ′) ]x=+∞
d x ∂x- |x---x′|- = dydz |x--x′| ′ = 0
x=-∞](elct172x.png)
となるので、結局、「定常電流の保存則」(3.2)を用いて
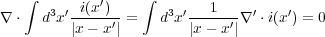
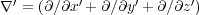 よって
よって
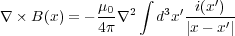
となります。この積分の計算ですが、少々面倒なので、難しいようでしたら結果だけ見てください。まず、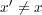 のと
き
のと
き
![( )
2 --1---- ∂2-- ∂2- -∂2 --1----
∇ |x - x′| = (∂x2 + ∂y2 + ∂z2 )|x - x′|
3 3[(x- x′)2 + (y - y′)2 + (z - z′)2]
= - -----′3 +----------------′5-----------
|x - x| |x- x |
= - ---3---+ ---3---
|x - x′|3 |x- x′|3
= 0](elct177x.png)
 中心で半径が微少量
中心で半径が微少量 の球
の球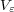 とそれ以外の領域
とそれ以外の領域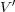 に分けると
に分けると![μ0 ∫ ( 1 )
∇ × B (x) = -4π- d3x′∇2 |x--x′| i(x′)
[∫ ( ) ∫ ( ) ]
= - μ0 d3x′∇2 ---1--- i(x ′)+ d3x′∇2 ---1--- i(x′)
4π Vε |x- x′| V′ |x- x′|](elct182x.png)
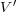 では常に
では常に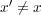 なので、
なので、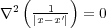 となり、消えてしまうので、問題は
となり、消えてしまうので、問題は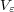 の積分だけになりま
す。今、
の積分だけになりま
す。今、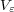 は極めて小さいので、その中だけを動く
は極めて小さいので、その中だけを動く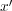 は限りなく
は限りなく に近いので、
に近いので、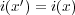 としてよいの
で
としてよいの
で
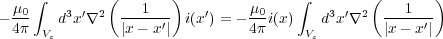
さらに、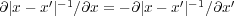 より
より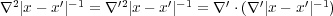 なの
で、
なの
で、
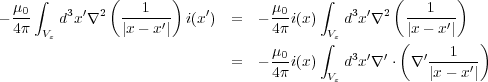
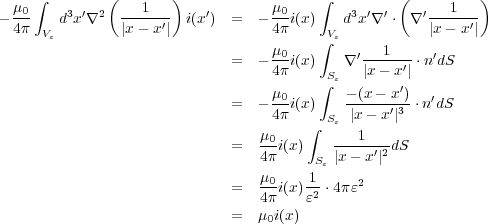
よって、
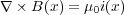 | (3.14) |
が得られます。これがもうひとつの磁場の基本法則「微分形のアンペールの法則」といいます。しかし、ここの目的だった マクスウェル方程式の四つ目
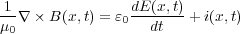
とは似ているけどちょっと違いますね。まず右辺の第一項がないし、また時間 を含む関数になっていません。微
分形のアンペールの法則は時間変化がない「定常電流の保存則」を使って導かれたので、当然時間
を含む関数になっていません。微
分形のアンペールの法則は時間変化がない「定常電流の保存則」を使って導かれたので、当然時間 を含
む形に一般化できません。実はそこが大きな問題なのです。それをどうするかは歴史的にも物理的にも大
きな山場なので、あとのお楽しみにとっておいて、先に残ったマクスウェル方程式の三つ目を導きましょ
う。
を含
む形に一般化できません。実はそこが大きな問題なのです。それをどうするかは歴史的にも物理的にも大
きな山場なので、あとのお楽しみにとっておいて、先に残ったマクスウェル方程式の三つ目を導きましょ
う。