Chapter 2
最小作用の原理とオイラー・ラグランジュ方程式
2.1 最小作用の原理
さて、「最小作用の原理」とは「物体の運動は作用を最小にするようにして決まる」というものです。では作用とはなん でしょうか?ってとこが気になりますが、ひとまず置いといてまず先ほどのオイラー・ラグランジュ方程 式1.4を
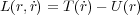
で解いてみます。ここで T は運動エネルギーで
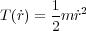
U はポテンシャルエネルギーで、力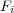 と
と
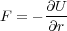
との関係があります。なので
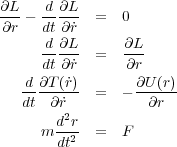
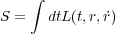
を最小にする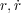 を見つける方程式だったわけです。つまり、力を
を見つける方程式だったわけです。つまり、力を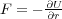 と書ける場合、
と書ける場合、

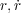 を導くわけで
す。まとめると
を導くわけで
す。まとめると 「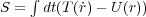 を最小にするように物体の運動は決まる」
を最小にするように物体の運動は決まる」
となるわけで、最小作用の原理の作用とはまさにこのSのことです。
まあ、と突然いわれても「運動エネルギーもポテンシャルエネルギーもニュートン運動方程式からでてきたもので
しょ?それを組み合わせて作用とか言われても。。しかも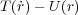 って何さ?
って何さ? なら全運動量だけどマ
イナスだと何を表すものなの?」と思うかも知れません。僕が昔そう思いました。
なら全運動量だけどマ
イナスだと何を表すものなの?」と思うかも知れません。僕が昔そう思いました。
しかし、とりあえず適当な L (以下ラグランジアンといいますが)例えば今の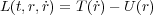 を仮定したな
らその積分の S を最小にするように物体の運動は定まる。つまり解析力学の公理は
を仮定したな
らその積分の S を最小にするように物体の運動は定まる。つまり解析力学の公理は
- 最小作用の原理
- 適当なラグランジアン L
- (慣性の法則)
の二つ(三つ)になるわけです。全宇宙の法則をしるためには我々は完璧なラグランジアンを見つければいいわけです。
(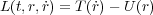 では電磁気のローレンツ力のような力を
では電磁気のローレンツ力のような力を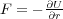 と書けない場合には不完全。それに
ついては後で)他にも解析力学のほうが数学的にきれいな形で書くことができたり、実際の計算が楽だっ
たりします。これだけの理由だと必ずしもニュートン力学より解析力学のほうが勝っているとは言いがた
いですが、量子力学ができ状況は大きく変わります。量子力学はいままでのニュートン物理とは大きく食
い違うものでしたが、量子力学でも「最小作用の原理」は適応されるのです。こうなってくると誰もが解
析力学の考え方こそが本質でそこからニュートン運動方程式が導けるのだ、と考えるようになったわけで
す。
と書けない場合には不完全。それに
ついては後で)他にも解析力学のほうが数学的にきれいな形で書くことができたり、実際の計算が楽だっ
たりします。これだけの理由だと必ずしもニュートン力学より解析力学のほうが勝っているとは言いがた
いですが、量子力学ができ状況は大きく変わります。量子力学はいままでのニュートン物理とは大きく食
い違うものでしたが、量子力学でも「最小作用の原理」は適応されるのです。こうなってくると誰もが解
析力学の考え方こそが本質でそこからニュートン運動方程式が導けるのだ、と考えるようになったわけで
す。
さらにラグランジアンは多数の質点をまとめても成り立ちます。今ポテンシャルを万有引力、また静電気力だとするな ら質点間の距離だけの関数なので
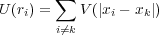
と書ける場合
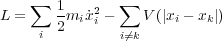 | (2.2) |
この L から各々の質点の運動が導かれるわけです。以下断りがなければ L といばこの L のことを指すことにしま す。
2.2 例 重力中での惑星の運動
さて、ニュートン運動方程式で惑星軌道を得るのにはずいぶん苦労しましたね(力学惑星の運動参照)。
これは極座標への微分の変換が面倒だったからです。なぜたいへんなのかと言えばニュートンの運動方程
式は基本的に x,y,z 座標(直交直線座標)で考えられているので極座標のような曲線座標に適用するには
一手間かかるわけです。しかし、オイラー・ラグランジュ方程式ではラグランジアン L さえわかっていれ
ば
どんな座標だろうと作用を最小にするように運動が決まる→方程式の座標がどんなのでもかまわない
というようにオイラー・ラグランジュ方程式では好きなように座標が取れます。今惑星の軌道を考える上で太陽の位置を原
点とした極座標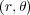 で惑星の質量を m、太陽の質量を M、重力定数を G とすると(ただし太陽は充分重いので動かない
ものとする)
で惑星の質量を m、太陽の質量を M、重力定数を G とすると(ただし太陽は充分重いので動かない
ものとする)
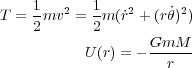
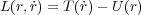 より
より
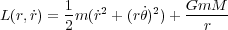
これから r に関するオイラー・ラグランジュ方程式は

 に関する式はとこの2式は惑星の運動で求めた運動方程式と同じです(式2.4は角運動量保存の式になってます)。以降の計算はそちら
を参照してください。
に関する式はとこの2式は惑星の運動で求めた運動方程式と同じです(式2.4は角運動量保存の式になってます)。以降の計算はそちら
を参照してください。とまあ、このようにオイラー・ラグランジュ方程式を使えばずいぶん簡単に運動方程式を求めることができまし た。複雑な力学の問題を解くなら断然オイラー・ラグランジュ方程式を使ったほうが便利なことは多いで す。

