Chapter 3
運動方程式の積分と保存量
さて、先ほど述べたように運動方程式は微分方程式なので滅多に解けません。それではあんまりなので運動方程式をあれこ れうまく変形して一部でも積分して時間変化しないうまい量を考え出しました。それを保存量といい、実は高校でならった 運動量やエネルギーがそうなのです。高校では突然に定義されたこれらの量ですが、どう運動方程式をいじると出てくるの か実際に見てみましょう。
3.1 運動量
運動量という量は高校でお馴染みかもしれませんが、なぜ運動量の変化が力と時間の積なのか、そもそも運動量ってなんな んだろうかと疑問に思った人もいるかと思います。そんな疑問にひとつの答えを示したいと思います。まず、とにかく運動 方程式を時間で積分してみます
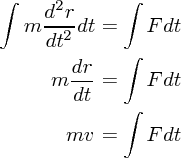
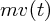 が力と時間の積(正確には積分)であることはわかりました。ただなんでこんな量を新たに
考えるのかといえば、単純に「便利」だからです。どう便利なのかというと、このあの有名な「運動量保存則」があるから
です。どういうことが具体的に計算してみましょう。
が力と時間の積(正確には積分)であることはわかりました。ただなんでこんな量を新たに
考えるのかといえば、単純に「便利」だからです。どう便利なのかというと、このあの有名な「運動量保存則」があるから
です。どういうことが具体的に計算してみましょう。
今二つの物体があって、特に重力などの力がかかっていない場合を考えます。そして時間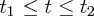 の間、互いに衝
突して力を受けたとします。このとき作用・反作用の法則よりお互いが受けた力は向きが逆で大きさが一緒であることはわ
かります。さて、この受けた力はそれぞれ
の間、互いに衝
突して力を受けたとします。このとき作用・反作用の法則よりお互いが受けた力は向きが逆で大きさが一緒であることはわ
かります。さて、この受けた力はそれぞれ
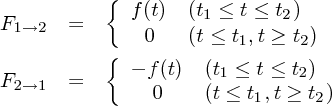
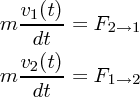
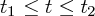 の間で積分すると
の間で積分すると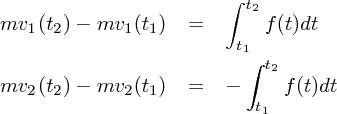
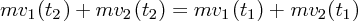 | (3.1) |
が得られます。これから衝突前と衝突後で全体の運動量 は変化しない、という事が言えます。つまり物体にお
互いの衝突による力以外の重力などの力(外力)がかかっていなければ、運動量は変わらないという「運動量保存則」が得
られます。こんな風になかなか解けない運動方程式を少しでも扱いやすくするため、運動量のような時間で変化しない量、
「保存量」を式をいじって見つけたかったのです。保存量を計算すれば直接微分方程式を解かなくても(高校物理でお馴染
みのように)ある程度情報を得ることができます。こういった意味では「運動量は単なる計算の都合上、
考え出されたもの」といってもいいでしょう。ただこの「都合上の量」が物理の本質に関わっていたので
す。
は変化しない、という事が言えます。つまり物体にお
互いの衝突による力以外の重力などの力(外力)がかかっていなければ、運動量は変わらないという「運動量保存則」が得
られます。こんな風になかなか解けない運動方程式を少しでも扱いやすくするため、運動量のような時間で変化しない量、
「保存量」を式をいじって見つけたかったのです。保存量を計算すれば直接微分方程式を解かなくても(高校物理でお馴染
みのように)ある程度情報を得ることができます。こういった意味では「運動量は単なる計算の都合上、
考え出されたもの」といってもいいでしょう。ただこの「都合上の量」が物理の本質に関わっていたので
す。
3.2 エネルギー
もうひとつ有名な保存量として忘れちゃいけないのがエネルギーです。なぜエネルギーは保存するのか?そもそもエネル ギーってなにか?という問いのひとつの答えとして「単なる運動方程式の保存量の一つ」とも言えるでしょう。高校ではエ ネルギーとは「力と距離の積」と習いましたが、なぜそんな量を考えるのか、なぜその量は保存するのか?という疑問が 残ったかと思います。それを解決したいと思います。
まず、運動方程式
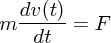
の両辺に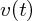 をかけます。これを時間で積分すると
をかけます。これを時間で積分すると
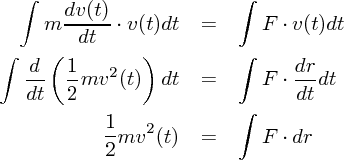
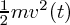 が確かに力と距離の積(積分)であることはわかりました。
ではこれがなんで保存するのかを述べるのにまず、次に述べる「ポテンシャルエネルギー」というものを考えま
す。
が確かに力と距離の積(積分)であることはわかりました。
ではこれがなんで保存するのかを述べるのにまず、次に述べる「ポテンシャルエネルギー」というものを考えま
す。
3.2.1 ポテンシャルエネルギー
さて、力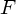 の積分ができたとすると
の積分ができたとすると
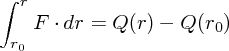
と書けますね。(これは当たり前のようですが実は力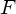 も距離
も距離 も今はベクトル量なので、数学的にはむしろこんな形に
かけることは珍しいんです。ただ現在見つかっている基本的な力はみなこうかけるのでここでは詳しく突っ込みませ
ん、ちなみにこうかける力のことを特に「保存力」と呼びます)今、のちのちのため
も今はベクトル量なので、数学的にはむしろこんな形に
かけることは珍しいんです。ただ現在見つかっている基本的な力はみなこうかけるのでここでは詳しく突っ込みませ
ん、ちなみにこうかける力のことを特に「保存力」と呼びます)今、のちのちのため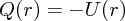 とマ
イナスをつけたものを考え、これを「ポテンシャルエネルギー」と呼びます。つまりポテンシャルエネル
ギーとは力の距離積分したものにマイナスをつけたものです。(実はポテンシャルエネルギーとは高校で
の位置エネルギーです)また、逆にポテンシャルエネルギーから力は、マイナスつけて微分すればいいの
で
とマ
イナスをつけたものを考え、これを「ポテンシャルエネルギー」と呼びます。つまりポテンシャルエネル
ギーとは力の距離積分したものにマイナスをつけたものです。(実はポテンシャルエネルギーとは高校で
の位置エネルギーです)また、逆にポテンシャルエネルギーから力は、マイナスつけて微分すればいいの
で
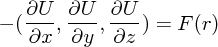
となります。これだと長ったらしいので以下のような省略記号をよく使います。
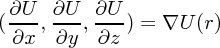
この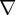 は「ナブラ(nabla)」と読みます。
は「ナブラ(nabla)」と読みます。
3.2.2 エネルギー保存則
さて、このポテンシャルエネルギーを使いもう一度運動方程式を先ほどのように積分します。
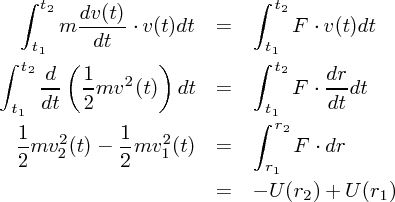
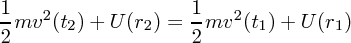 | (3.2) |
これから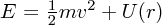 が時間で変化しない、エネルギー E が保存することがわかりました。この考え方から
いえばエネルギーもまた運動方程式を解くために計算が楽になるよう定義した道具の一つといえるでしょ
う。
が時間で変化しない、エネルギー E が保存することがわかりました。この考え方から
いえばエネルギーもまた運動方程式を解くために計算が楽になるよう定義した道具の一つといえるでしょ
う。
3.3 角運動量
つづいて角運動量というものを導入しますがそのためにまず、ベクトル積というものを考えます。
3.3.1 ベクトル積
いま、ベクトル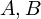 があるとします。そのベクトル積は
があるとします。そのベクトル積は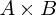 と書き、これは大きさが
と書き、これは大きさが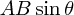 で、方向が
で、方向が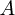 と
と
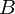 に垂直で
に垂直で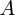 から
から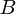 に回して右ねじが進む方向を向いているベクトルです。つまり、それぞれの単位ベクトル
に回して右ねじが進む方向を向いているベクトルです。つまり、それぞれの単位ベクトル
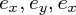 に対して
に対して
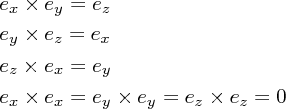
が成り立ちます。これから、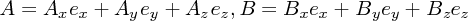 は
は
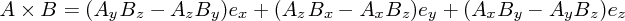
と書けます。
さて、運動方程式
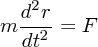
に左から先程のベクトル積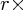 をかけると
をかけると
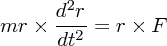
さて、この左辺は、角運動量
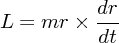 | (3.3) |
の微分
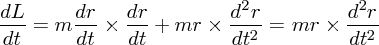
と等しいです。ここで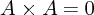 を使いました。つまり先程の式は
を使いました。つまり先程の式は
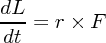
となります。この右辺の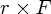 を「トルク」と呼びます。さて、こんな量を考えて何がうれしいかというと世の中の基本
的な力はみな「中心力」という力です。これはどんな力かというと、ある一点から引っ張られたり反発したりする力です。
例えば太陽に引っ張られる重力です。数学でいえばある一点(例えば太陽)を原点とすると
を「トルク」と呼びます。さて、こんな量を考えて何がうれしいかというと世の中の基本
的な力はみな「中心力」という力です。これはどんな力かというと、ある一点から引っ張られたり反発したりする力です。
例えば太陽に引っ張られる重力です。数学でいえばある一点(例えば太陽)を原点とすると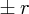 の方向をもった力のこと
です。例えば太陽との重力は
の方向をもった力のこと
です。例えば太陽との重力は
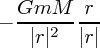
と書けます。ここで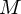 は太陽の質量、
は太陽の質量、 が太陽からの距離です。さて、この中心力の場合
が太陽からの距離です。さて、この中心力の場合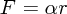 となるので、トルク
は
となるので、トルク
は
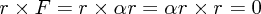
なので
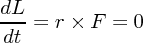
よって中心力では
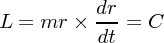 | (3.4) |
と角運動量は保存されます。高校ではなじみのないこの保存量ですが、物理の概念としてとても重要な量で す。
