Chapter 3
保存量と対称性(ネーターの定理)
つづいて、オイラー・ラグランジュ方程式をつかって保存量を見ていきましょう。
保存量とはたとえばエネルギーや運動量などの時間変化しないでいつでも同じ値になるものでしたね。これを探すには時間
微分が0になるものを見つければいいですが、その方法はニュートン運動方程式では基本的に片っ端から調べるしかなかっ
たのに対して、解析力学では定理として方法があり、しかもこの考え方は量子力学などにも応用される現代物理の大きな
テーマにもなっています。
3.1 循環座標
一番シンプルな保存量の見つけ方は循環座標を見つけることです。循環座標とはラグランジアン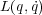 に
に が含まれて
いないのような(
が含まれて
いないのような(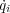 は含まれいている)座標のことです。先ほどの惑星の運動の場合は
は含まれいている)座標のことです。先ほどの惑星の運動の場合は
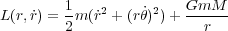
なので、 が循環座標にあたるわけです。さて循環座標ではどうなるかといえば、オイラー・ラグランジュ方程式
が
が循環座標にあたるわけです。さて循環座標ではどうなるかといえば、オイラー・ラグランジュ方程式
が
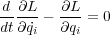
なのでラグランジアン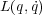 に
に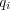 が含まれていないなら左辺第二項は0となり
が含まれていないなら左辺第二項は0となり
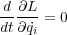
より時間微分が0なので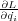 は保存量になるわけです。先ほどの惑星の運動では式2.4の角運動量がそれ
にあたるわけです。解析力学ではより多くの循環座標があるように座標系を選べば計算が楽になるわけで
す。
は保存量になるわけです。先ほどの惑星の運動では式2.4の角運動量がそれ
にあたるわけです。解析力学ではより多くの循環座標があるように座標系を選べば計算が楽になるわけで
す。
3.2 ネーターの定理
さて、循環座標をとれば保存量がわかるというわけなんですが、「その循環座標をどうやって見つければいいのか?」とい
う疑問が湧いてきます。そのため、保存量を見つける方法といてもっと一般的(数学的)な定理があります。それがネー
ターの定理です。具体的にどういうものかというと
「座標を少しだけ変えたもの(無限小変換)
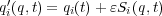
を考え( は無限小の定数、
は無限小の定数、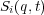 は任意の関数)、ラグランジアン
は任意の関数)、ラグランジアン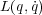 を
を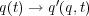 と置き換えても形が変
わらないとき
と置き換えても形が変
わらないとき
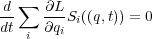 | (3.1) |
が成り立つ(保存量になる)」
と言うものなんですが、いろいろわかりにくいですよね。とりあえず順を追って説明していきます。
まず、「無限小変換って何さ?」というととりあえず今座標を変えたいんです。そしてほんのちょっとだけ変えたのな ら微分を使って表せるので便利なわけです。ほんのちょっと変えたものでも無限に繰り返せば有限の変換に戻るわけなん で、とりあえず便利なちょっとだけかえるもの「無限小変換」を考えるわけです。そしてそのちょっと変えたものは「元の やつ」+「ちっちゃな変化」
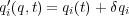
とかけるわけで、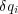 は小さな値の q や t の関数だから(座標を他の座標に変えるだけなんだから他の変数がでてきませ
んよね)小さい定数
は小さな値の q や t の関数だから(座標を他の座標に変えるだけなんだから他の変数がでてきませ
んよね)小さい定数 を使い
を使い
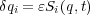
と書き直してもいいわけです。なんでこんな形にしたかというのはあとで具体的な例を見たときにわかると思いま
す。
続いて、「ラグランジアン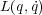 を
を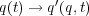 と置き換えても形が変わらない」というのは単純に
と置き換えても形が変わらない」というのは単純に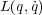 の
の
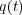 に
に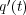 を代入し計算したものと代入する前のやつが同じいうことです。例えばポテンシャルがない 1 次元の運動の
とき
を代入し計算したものと代入する前のやつが同じいうことです。例えばポテンシャルがない 1 次元の運動の
とき
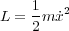
ですが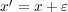 を考えると加えるのは定数なの代入しても
を考えると加えるのは定数なの代入しても

さて、今対称性があるかどうかわからない無限小変換をとりあえずしたとします。それでラグランジアンがどれだけ変化し たかは
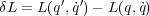
とかけますね。さて今変化は充分小さいので微分を使い
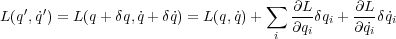
よって
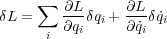
ここで
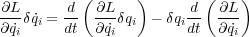
なので結局
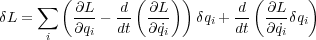
しかしよく見てみると右辺第一項の括弧内はオイラー・ラグランジュ方程式1.4になっていますね。よって 0 とな り
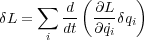
そしてもし対称性があるならラグランジアンは一緒つまり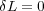 なので
なので
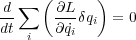
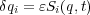 と置き換えると
と置き換えると は定数なので
は定数なので

と式3.1が導けたわけです。
3.3 対称性と保存則
3.3.1 空間平行移動対称性と運動量
空間を平行にずらす変換
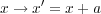
に対してラグランジアンは
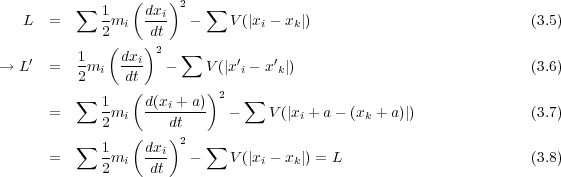
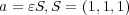 とすると
とすると
3.3.2 空間回転対称性と角運動量
空間の回転を表す変換は
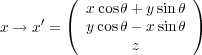
これを無限小変換とすると で
で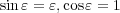 から
から
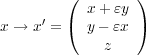 | (3.12) |
この変換に対して
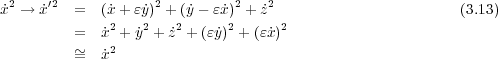
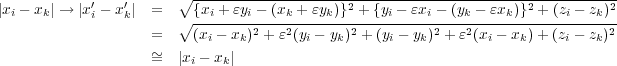
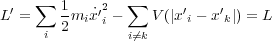
で不変、よってネーターの定理から
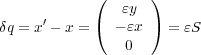
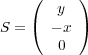
で

3.3.3 時間の平行移動対称性とエネルギー
さて、今までは対称性をラグランジアンで考えてきましたが運動は作用 S、ラグランジアン L の時間積分を最小にするよう に決まるわけですから実は作用 S の対称性が大切なわけです。ただラグランジアン L が対称ならその積分の作用も対称なの で問題なかったわけです。
今、時間の平行移動を考えてみたいと思います。
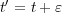
このとき、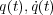 の位置座標は変えないようにします。(そうしないと対称性は
の位置座標は変えないようにします。(そうしないと対称性は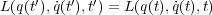 が成
り立つこと、つまり L が時間変化しない、保存量という厳しすぎる条件になってしまいますので)つまり時間がずれた分を
が成
り立つこと、つまり L が時間変化しない、保存量という厳しすぎる条件になってしまいますので)つまり時間がずれた分を
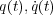 は逆にずらして
は逆にずらして

この変換に対して作用 S が対称だとすると(L が対称だけだと今回は t が変化するので積分区間の扱いができなくて先 ほどまでのネーターの定理では議論できない)
 | (3.20) |
が得られます。(証明は物理のかぎしっぽ http://hooktail.sakura.ne.jp/analytic/energyDefinitionConservation/を参照 してください)
具体的に
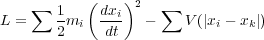
のとき
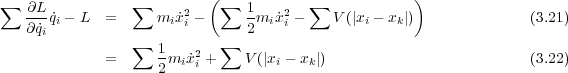
- 空間の平行移動対称性 → 運動量保存
- 空間の回転対称性 → 角運動量保存
- 時間の平行移動対称性 → エネルギー保存
という美しい法則が解析力学では明らかになります。
