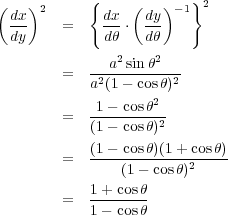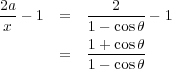Chapter 1
最速降下曲線
「最小作用の原理」を語る上で歴史的経緯として、また格好の例題をして最速降下曲線の問題が挙げられます。さて、最速 降下曲線とは適当な二点(高さに差がある)を、ボールが最も早く転がり抜けるように引いた曲線のことです。この 問題はベルヌーイが懸賞問題として発表し、そしてそれを一日でニュートンは解いてしまったといわれま す。
この問題を解く方法は割りとシンプルです。まず、今適当な曲線をとりあえず考えます。どんなものでもよく「とりあ えず」考えます。そしてこの曲線にそってボールが転がるときにかかる時間を求めます。これはわりと簡単です。まず、 x まで落ちたときの速度はエネルギー保存より

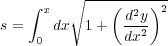
とかけるのでかかる時間は
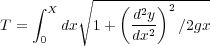 | (1.2) |
と書けます。ここから最速降下曲線を見つけるにはつまり、このTが最小になるような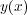 を見つけてやればいいわけで
す。ここで今のちのちのためより一般的な場合を考えて見ましょう。
を見つけてやればいいわけで
す。ここで今のちのちのためより一般的な場合を考えて見ましょう。
1.1 オイラー・ラグランジュ方程式
さて今
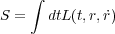
というSを最小にする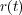 を求めたいとします。
を求めたいとします。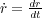 、
、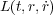 は
は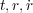 の任意の関数です。今Sだとか L だとか
x が t に変わっているのだとかはのちのちのちわかるので今は深く気にしないでください。さてSを最小にするような
の任意の関数です。今Sだとか L だとか
x が t に変わっているのだとかはのちのちのちわかるので今は深く気にしないでください。さてSを最小にするような
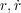 があったとします。そのときそれぞれちょっとずつずらして
があったとします。そのときそれぞれちょっとずつずらして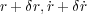 としたときのSを
としたときのSを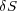 とする
と、
とする
と、
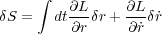 | (1.3) |
とかけますが、さて今Sを最小にするような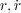 付近では
付近では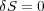 となります。それは微分で極値を求めると
きに微分したものが0となる点を探すのと同じで、Sを最小にするような
となります。それは微分で極値を求めると
きに微分したものが0となる点を探すのと同じで、Sを最小にするような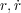 付近ではSの値はくぼ地
にはまっている状態でほかの場所と違い少々ずれても変わらないわけです。つまり求める
付近ではSの値はくぼ地
にはまっている状態でほかの場所と違い少々ずれても変わらないわけです。つまり求める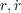 の方程式
は
の方程式
は
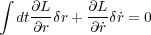
となります。さて今積分の始点終点では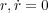 として上の式を
として上の式を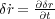 を使って部分積分で整理する
と
を使って部分積分で整理する
と
![∫
dt∂L-δr+ ∂L-δ˙r = 0
[ ] ∫ ∂r ∂r˙
∂L-δr + dt∂L-δr - d-∂L-δr = 0
∂r˙ ( ∂r dt∂r)˙
∫ ∂L- -d∂L-
dt ∂r - dt ∂˙r δr = 0](analy21x.png)
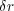 は好きに動かせる微少量なので右辺が0になるためには () の中が0でないといけないので
は好きに動かせる微少量なので右辺が0になるためには () の中が0でないといけないので
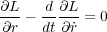 | (1.4) |
この式を「オイラー・ラグランジュ方程式」といいます。
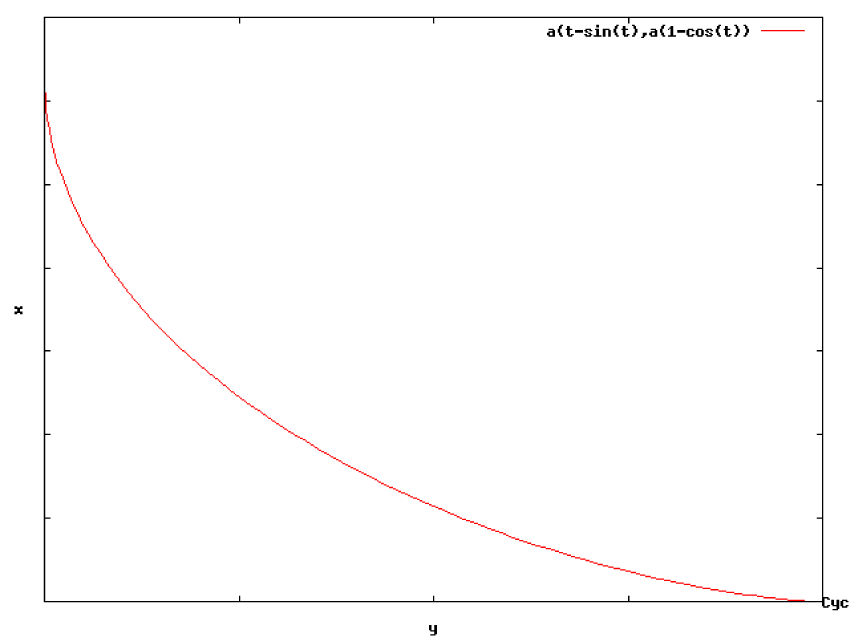
1.2 サイクロイド曲線
さて、最速降下曲線の話にもどりましょう。さきほどのオイラー・ラグランジュ方程式1.4で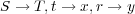 と置き
直し式1.2の積分の中身
と置き
直し式1.2の積分の中身
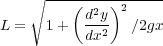
を代入し、整理すると
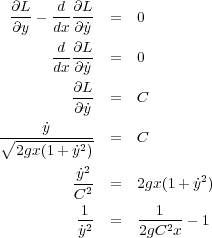
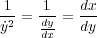
なのと、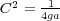 という a を使うと方程式は
という a を使うと方程式は
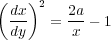 | (1.5) |
という形にかけます。実はこの方程式の解はサイクロイド曲線になっています。方程式から直接求めるのは難しいのでサイ クロイドの式

まず
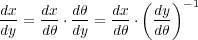
なので式1.5の右辺は