2 高次の差分法 (Runge-kutta 法)

Chapter 2
高次の差分法 (Runge-kutta 法)

2.1 Toyler 法

一般に

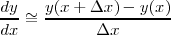
dy-~= y(x-+-Δx)-- y(x) dx Δx

という形に近似して計算する方法を差分法といいます。もっともシンプルな形はオイラー法ですがこれをもっと精度のよい近似にするには

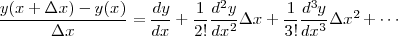
y(x + Δx)- y(x) dy 1 d2y 1 d3y 2 ------Δx------- = dx-+ 2!dx2Δx + 3!dx3Δx + ⋅⋅⋅

と Toyler （テイラー）展開したものを使えばいいのです。これを Toyler 法といいます。たとえば２次までとると

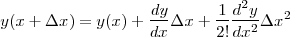
2 y(x + Δx) = y(x) + dyΔx + -1d-yΔx2 dx 2!dx2

です。ここで

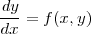
dy- dx = f(x,y)

から

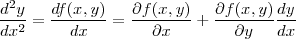
2 d-y2 = df(x,y)= ∂f-(x,y) + ∂f(x,y)dy- dx dx ∂x ∂y dx

というふうに次々にｙのｎ回微分が求まるので基本的に何次でも計算できます。ただ、実はこのテイラー法はあまり使われません。何でかというと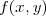 $f (x,y)$ が簡単なときはいいですが複雑な場合計算がすごく面倒になります。そしてもうひとつは、そんな面倒な計算をしないで済む方法が別にあるからです。

2.2 Runge-kutta 法

さて、上で言った別の方法というのがこの Runge-kutta （ルンゲ - クッタ）法です。この方法の目的は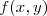 $f(x,y)$ の微分を使わずに次数を上げることです。そのためにちょっと数式をいじりますががんばってついてきてください。これから２次の Runge-kutta （ルンゲ - クッタ）法を導きますが以下

h = Δx xn = x0 +nh

とします。まず、計算する式を今

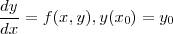
dy ---= f(x,y),y(x0) = y0 dx

だとすると

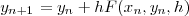
yn+1 = yn + hF (xn,yn,h)

と差分法にするにあたって

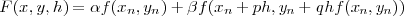
F(x,y,h) = αf (xn,yn) +βf (xn + ph,yn + qhf(xn,yn))

という適当な $f(x,y)$ の足し合わせにしてやります。なぜこの形かと言えばこうするとうまくいくからなんです（笑）さて, まず $f (xn + ph,yn + qhf(xn,yn))$ を展開します

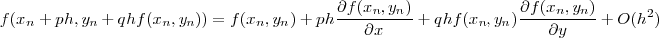
∂f(xn,yn) ∂f(xn,yn) f(xn + ph,yn + qhf(xn,yn)) = f(xn,yn)+ ph---∂x----+ qhf(xn,yn)---∂y----+ O (h2)

これを元の式にいれ

yn+1 = yn + hF(xn,yn,h) [ ( )] = yn + h αf(xn,yn)+ β f(xn,yn)+ ph∂f-(xn,yn) + qhf (xn,yn)∂f-(xn,yn) + O(h2) ∂x ∂y = y + h(α+ β)f(x ,y )+ h2(βp∂f(xn,yn)+ βqf(x ,y )∂f(xn,yn))+ O (h3) n n n ∂x n n ∂y

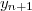さて、ここで $yn+1$ の本当の展開は

2 2 yn+1 = yn + hdyn + h dyn-+ O (h3) dx 22! dx2 = yn + h-df-+ h [∂f-+ f∂f-]+ O(h3) dx 2!∂x ∂y

よって２次まで一致させるには

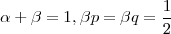
α + β = 1,βp = βq = 1 2

よって

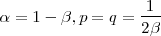
-1- α = 1- β,p = q = 2β

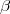ここで $β$ は任意です。そのため同じ２次のルンゲ - クッタでもいくつか存在します。ふつう 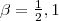$β = 12,1$ です。

具体的に書くと、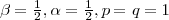 $β = 12,α = 12,p = q = 1$ の場合

1 yn+1 = yn +-h [f(xn,yn)+ f(xn + h,yn + hf(xn,yn))] 2

なので実際の計算手順は

yｯn+1 = yn + hf(xn,yn) y*n+1 = yn + hf(xn+1,ｯyn+1) ｯy + y* yn+1 = -n+1---n+1- 2

となります。これをつかって早速、オイラー法でいまいちだった重力の問題

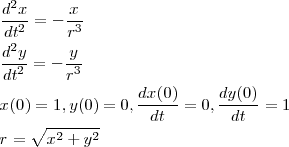
2 d-x= - x- dt22 r3 d-y= - y- dt2 r3 x (0) = 1,y(0) = 0, dx(0) = 0, dy(0)-= 1 ∘ ------- dt dt r = x2 + y2

を解いてみましょう。このソースはこちらです

#include <stdio.h>
#include <math.h>

int main(void){
double x[3] ={1,0,0};
double u[3] ={0};
double y[3] ={0};
double v[3] ={1,0,0};
int k;

for(k=1;k <= 100; k++){
  u[1] =u[0]+ -0.2 * x[0] / sqrt(y[0]*y[0]+x[0]*x[0]);
  x[1] =x[0]+ 0.2 * u[0];
  v[1] =v[0]+ -0.2 * y[0] / sqrt(y[0]*y[0]+x[0]*x[0]);
  y[1] =y[0]+ 0.2 * v[0];
  u[2] =u[0]+ -0.2 * x[1] / sqrt(y[1]*y[1]+x[1]*x[1]);
  x[2] =x[0]+ 0.2 * u[1];
  v[2] =v[0]+ -0.2 * y[1] / sqrt(y[1]*y[1]+x[1]*x[1]);
  y[2] =y[0]+ 0.2 * v[1];
  u[0] =(u[1]+u[2])/2;
  x[0] =(x[1]+x[2])/2;
  v[0] =(v[1]+v[2])/2;
  y[0] =(y[1]+y[2])/2;

  if(k%2==0) printf("%f %f\n",x[0],y[0]);
}
return 0;
}

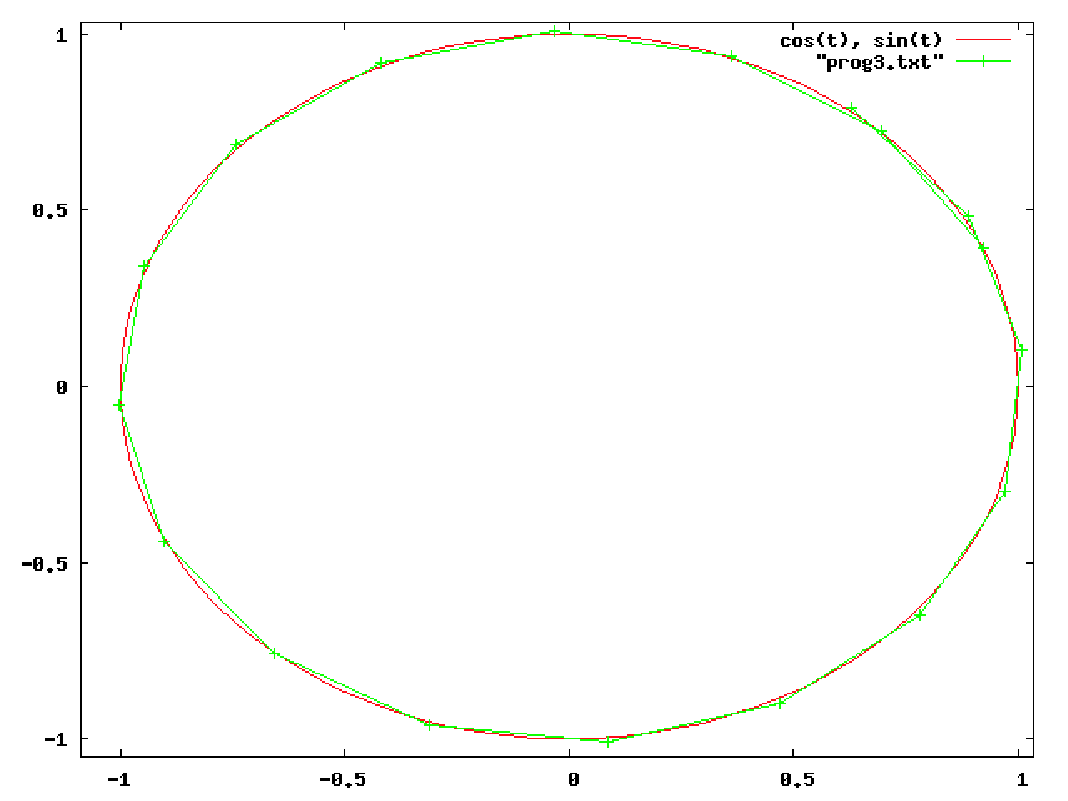
その結果はこちら

Figure 2.1:

２次の RK 法

結果は明らかですね。オイラー法に比べるとメッシュの幅が一緒なのにこれほど違うんです。実際の物理でも RK 法はよく使われています。

[次へ][前へ][目次]

物理の大事な骨の部分だけを独自にまとめましたサイトですご意見ご感想はこちらまで（「」内に@gmail.comを付けてください）　「ysdswallow」
top page	微分・積分のまとめ	ニュートン力学のまとめ
電磁気のまとめ	解析力学のまとめ	数値計算（微分方程式）のまとめ
おすすめ参考書等紹介

Chapter 2高次の差分法 (Runge-kutta 法)

2.1 Toyler 法

2.2 Runge-kutta 法

Chapter 2
高次の差分法 (Runge-kutta 法)