物理の小さい余白 物理の大事な骨の部分だけを独自にまとめましたサイトです
ご意見ご感想はこちらまで（「」内に@gmail.comを付けてください）　「ysdswallow」
top page 微分・積分のまとめ ニュートン力学のまとめ
電磁気のまとめ 解析力学のまとめ 数値計算（微分方程式）のまとめ
おすすめ参考書等紹介

[前へ][目次]

Chapter 3
高次の Runge-Kutta 法

２次より高次の RK 法は同じように

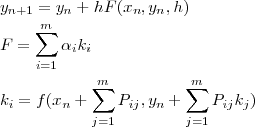
y = y + hF (x ,y ,h) n+1 m n n n F = ∑ αiki i=1 ∑m m∑ ki = f(xn + Pij,yn + Pijkj) j=1 j=1
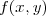というふうにf(x,y) を適当に組み合わせることで得られます。ここで以下
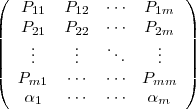
( ) P11 P12 ⋅⋅⋅ P1m || P21 P22 ⋅⋅⋅ P2m || || .. .. ... .. || |( . . . |) Pm1 ⋅⋅⋅ ⋅⋅⋅ Pmm α1 ⋅⋅⋅ ⋅⋅⋅ αm

といふうにｍ＋１行ｍ列の行列の形（Stetter の行列表現）で高次の RK 法を紹介していきます。

3.1 ２次の RK 法

先ほどやったやつですがこの行列で表すと

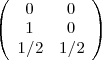
( ) 0 0 ( 1 0 ) 1∕2 1∕2

また、さきほど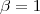β = 1 の場合は

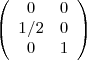
( 0 0 ) ( 1∕2 0 ) 0 1

となります。

3.1.1 ３次の RK 法

( 0 0 0 ) | 1∕2 0 0 | |( - 1 2 0 |) 1∕6 4∕6 1∕6

が３次の RK 法です。もちろん係数は代表的なものであって、これが唯一ではありません。ただ、３次はあまり使われませ ん。それは手間や精度などを考慮すると４次のほうがお得だからです。

3.2 ４次の RK 法

４次では例えば

( ) 0 0 0 0 || 1∕2 0 0 0 || || 0 1∕2 0 0 || ( 0 0 1 0 ) 1∕6 2∕6 2∕6 1∕6

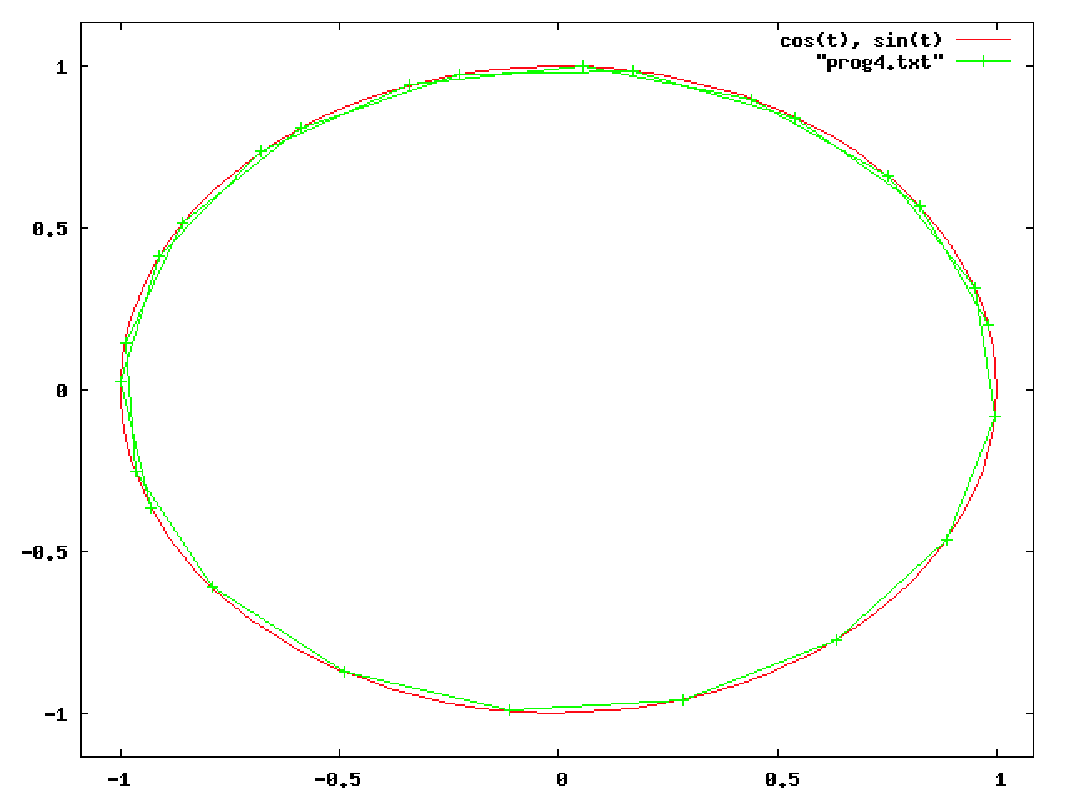
のようなものが有名です。４次の RK 法はかなりよく使われるものです。ためしにこれであの

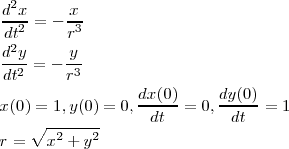
d2x x dt2 = - r3 d2y y --2 = --3 dt r dx(0) dy(0) x (0) = 1,y(0) = 0,---- = 0,-----= 1 ∘ ------- dt dt r = x2 + y2
を解いてみましょう。具体的な計算手順は
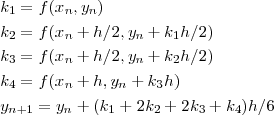
k = f(x ,y ) 1 n n k2 = f(xn + h∕2,yn + k1h∕2) k3 = f(xn + h∕2,yn + k2h∕2) k4 = f(xn + h,yn + k3h) y = y + (k + 2k + 2k + k )h∕6 n+1 n 1 2 3 4
となります。このソースは
/*四次RK法*/  
 
#include <stdio.h>  
#include <math.h>  
 
int main(void){  
 double x =1;  
 double kx[5] ={0};  
 double u =0;  
 double ku[5] ={0};  
 double y =0;  
 double ky[5] ={0};  
 double v =1;  
 double kv[5] ={0};  
 double h;  
 int k,t;  
 
 for(k=0;k < 100; k++){  
  for(t=0;t <=3;t++){  
   if(t<=2) h=0.1;  
   else h=0.2;  
   ku[t+1] =- (x+h *kx[t]) / sqrt((y+h *ky[t])*(y+h*ky[t])+(x+h *kx[t])*(x+h *kx[t]));  
   kx[t+1] = u+h *ku[t];  
   kv[t+1] = -(y+h *ky[t]) / sqrt((y+h *ky[t])*(y+h*ky[t])+(x+h *kx[t])*(x+h *kx[t]));  
   ky[t+1] =  v+h *kv[t];  
  }  
 
  u =u+(ku[1]+2*ku[2]+2*ku[3]+ku[4])*0.2/6;  
  x =x+(kx[1]+2*kx[2]+2*kx[3]+kx[4])*0.2/6;  
  v =v+(kv[1]+2*kv[2]+2*kv[3]+kv[4])*0.2/6;  
  y =y+(ky[1]+2*ky[2]+2*ky[3]+ky[4])*0.2/6;  
 
  if(k%2==0) printf("%f %f\n",x,y);  
 }  
 return 0;  
}

です。この結果が

PIC

Figure 3.1: ４次の RK 法

です。点の位置はほぼ理論値と一致していますね。確かにこの４次の RK 法がよく使われる理由がわかっていただける かと思います。

[前へ][目次]