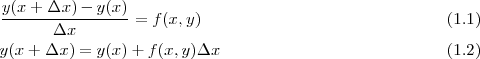Chapter 1
差分法 (Euler 法)
1.1 Euler 法
物理の基本的な式はみな微分方程式です。ニュートンの運動方程式も量子力学のシュレディンガー方程式もそうです。そ れで、ここではコンピュータを使ってどうやって微分方程式を計算するのかを簡単に紹介したいと思いま す。
さて、最も簡単な形としてオイラー(Euler)法というものがあります。まずもっとも簡単な微分方程式として例え ば
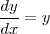
のように y の x での微分が x,y の関数でかけているとき
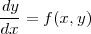
を考えていきます。このままでは当然コンピュータには計算させられません。そのためにはなんとか電卓で計算できる形、 つまり四則演算の形にしてやらなければいけません。さて、それにはなにより微分のところがどうにもなりませんね。そも そも微分とは
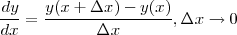
でした。これから0にはできないけども出来うる限り小さい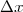 を使えば
を使えば
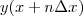 といったように y をどんどん求めていくことができます。これが
「Euler 法」です。実に簡単ですね。ためしに
といったように y をどんどん求めていくことができます。これが
「Euler 法」です。実に簡単ですね。ためしに
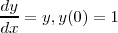
で計算してみましょう。この式の解は
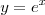
なので、今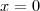 から1まで計算するとなると本当の答えは
から1まで計算するとなると本当の答えは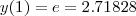 となるはずです。さて、この計算のた
めの C 言語でのプログラムのソースはこちらです。
となるはずです。さて、この計算のた
めの C 言語でのプログラムのソースはこちらです。
/*Euler法の練習*/
#include <stdio.h> int main(void){ double y=1.0; /*yの初期値は1です*/ double x=1000; /*この逆数がメッシュの大きさです*/ long i; for(i=1;i <= x;i++){ y += (1/x) * y; } printf("%f\n",y); /*結果を表示します*/ return 0; } |
このソースでは基本的に
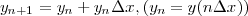
を繰り返しです。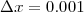 にして、 x=0 から1までなので上の式を 1,000 回繰り返したのですが、ここで問題なの
が
にして、 x=0 から1までなので上の式を 1,000 回繰り返したのですが、ここで問題なの
が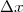 の値(以下メッシュという)をいくつにするかです。理論的にはメッシュをできるだけ小さくしたほうが
実際の微分に近づくわけだからそのほうがいいんですが、当然0にはできないしまた、メッシュを小さく
すればするほど計算回数が多くなり時間がかかってしまいます。
の値(以下メッシュという)をいくつにするかです。理論的にはメッシュをできるだけ小さくしたほうが
実際の微分に近づくわけだからそのほうがいいんですが、当然0にはできないしまた、メッシュを小さく
すればするほど計算回数が多くなり時間がかかってしまいます。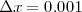 のこのソースでは結果は
2.716924 と誤差は 0.05 %というところです。メッシュの大きさと真値との誤差をグラフにしたのが次の図で
す。
のこのソースでは結果は
2.716924 と誤差は 0.05 %というところです。メッシュの大きさと真値との誤差をグラフにしたのが次の図で
す。
です。縦軸に誤差の%の対数、横軸がメッシュの幅の対数です。これからともに対数を取ったものは直線になっ ていることがわかると思います。この場合はかなり幅の小さいメッシュにしても時間はそれほどかかりま せんが、もっと複雑な式の場合は誤差と時間の兼ね合いを考えてメッシュの幅を決める必要があるでしょ う。
1.2 二次の微分方程式
さて、代表的な物理の方程式といえばニュートンの運動方程式
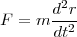
ですが、これは二回微分の式です。これに限らず二回微分の方程式は物理では大変多いです。一般に二回微分の 式
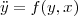
を Euler 法で計算するにはまず、yの一回微分を新たに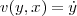 という関数だと考え
という関数だと考え
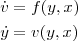
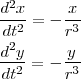
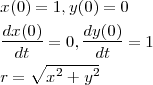
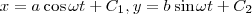
を代入して計算してやればすぐに半径1、中心0の円であることがわかります。ではさっそくこの式をオイラー法で計算し
ましょう。ソースは変数が増えるのでややこしくなりますがこうです。
/*Euler法 メッシュの幅は0.2としt=20まで計算する*/
#include <stdio.h> #include <math.h> int main(void){ double x =1; double u[2] ={0}; double y =0; double v[2] ={1}; /*u,vはそれぞれx,yの一回微分*/ int k; for(k=0;k < 1000; k++){ u[1] =u[0]+ -0.02 * x / sqrt(y*y+x*x); v[1] =v[0]+ -0.02 * y / sqrt(y*y+x*x); /*u,vは二回使うので一時的な保存先としてu(v)[1]を使う*/ x += 0.02 * u[0]; y += 0.02 * v[0]; u[0]=u[1]; v[0]=v[1]; if(k%20==0) printf("%f %f\n",x,y); /*20回に一回だけ結果を表示させる*/ } return 0; } |
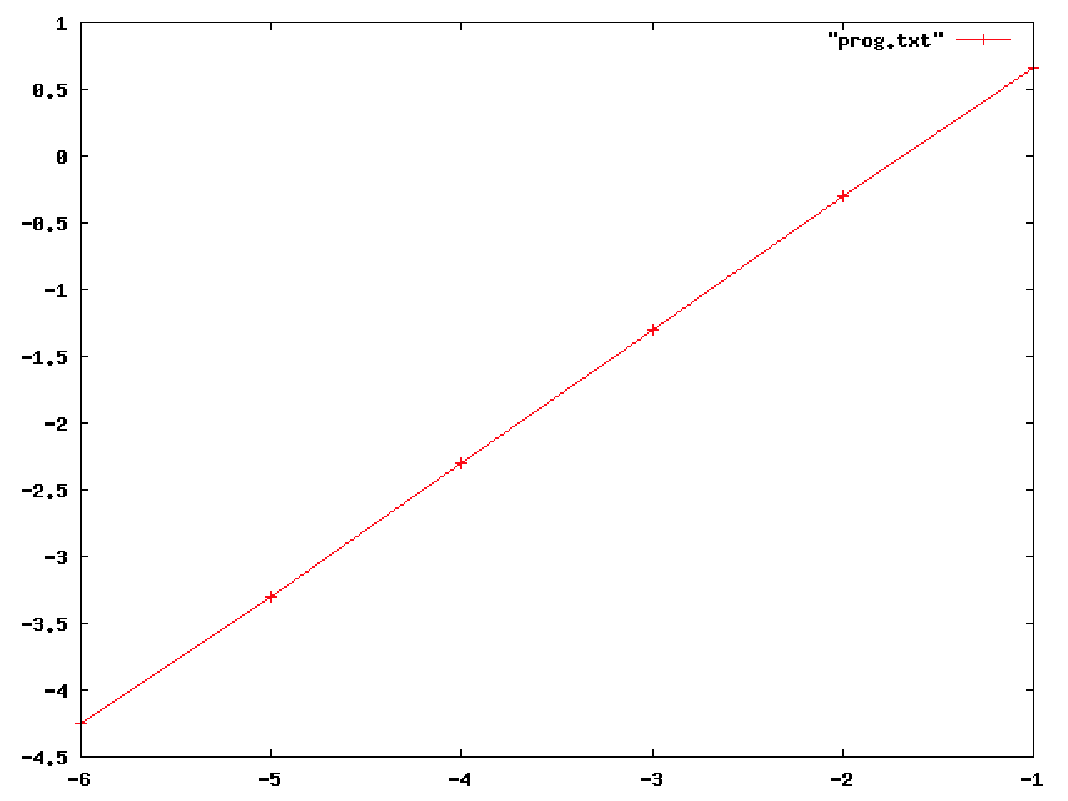
このソースでの計算は
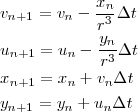
赤い線が理論値で緑が計算結果です。これははっきりいって悲惨ですね。もちろんメッシュを小さくすればマシにな りますがだんだん外に膨らんでいくのは変わりません。これはオイラー法の欠陥なのです。これで地球の 100 年後を計算すれば太陽系から離脱してしまいます。そこで次にもっと精度の高い計算方法を紹介しま す。