Chapter 4
惑星の運動
さて、今までに出した保存則をうまく使ってニュートン運動方程式の花形、惑星の運動を考えて見ましょう。今太陽は充分
重いのでその位置は動かないで原点にあると仮定して考えていきます。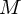 を太陽の質量、
を太陽の質量、 を太陽からの距離、惑星の
質量を
を太陽からの距離、惑星の
質量を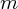 とすると運動方程式は
とすると運動方程式は
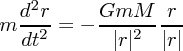 | (4.1) |
となります。ここで今力は太陽の方向、つまり原点の向きにしか働かないので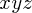 座標で考えるより極座標で考えたほう
が便利です。
座標で考えるより極座標で考えたほう
が便利です。
さて、しかしここで問題なのが微分です。ニュートン運動方程式は基本的に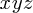 座標で考えられています。なので座
標を変えたときは微分の部分が変化します。具体的に見てみましょう。極座標(2次元)と
座標で考えられています。なので座
標を変えたときは微分の部分が変化します。具体的に見てみましょう。極座標(2次元)と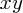 座標の関係
は
座標の関係
は
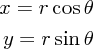
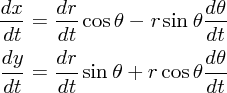
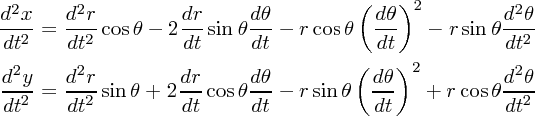

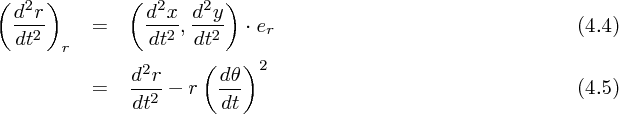
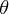 方向は
方向は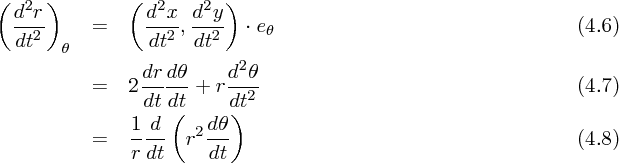
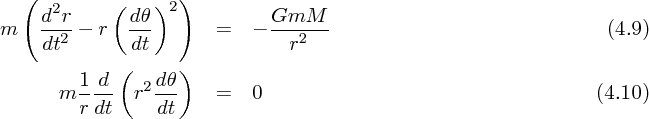
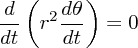
ですが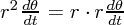 は r かける
は r かける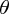 方向の速度、つまり角運動量(から質量を割ったもの)になっています。今これが時
間によらず一定なのでその値を
方向の速度、つまり角運動量(から質量を割ったもの)になっています。今これが時
間によらず一定なのでその値を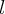 と置くと
と置くと
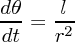 | (4.11) |
となります。
さて、もうひとつの式
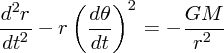
ですが、今この式から惑星の楕円運動が出てくればうれしいわけなので時間ごと r の値より実は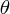 ごとの r の値のほうが
やりやすいわけです。なのでまず、時間微分を
ごとの r の値のほうが
やりやすいわけです。なのでまず、時間微分を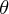 微分に書き換えをします。
微分に書き換えをします。


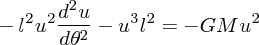 | (4.19) |
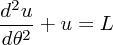 | (4.20) |
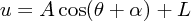 | (4.21) |

まず、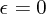 のとき r は
のとき r は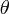 に依存しないわけですからどの
に依存しないわけですからどの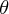 でも r 一定、つまりこれは円軌道になります。では
でも r 一定、つまりこれは円軌道になります。では
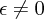 のとき、
のとき、
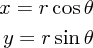
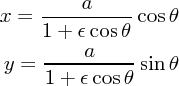
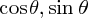 について解き直し
について解き直し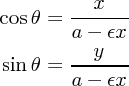
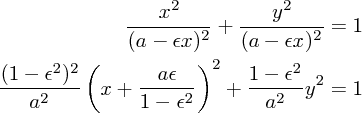
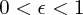 (
(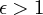 )のときは楕円(双曲線)の式
)のときは楕円(双曲線)の式
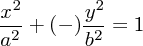
を満たしていることがわかります。このようにニュートンは惑星の運動さえも証明し物理の夜明けを華々しく飾ったので す。
