Chapter 2
微分方程式としての運動方程式
さて、高校ではこれで終わりでこの運動方程式を直接計算することは少ないかと思います。それにはこの書き方に問題があ
るのです。質量はこれでいいとして、まず力 F は当然方向を持った量、そうベクトルなので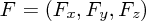 としてお
かなければなりません。ここで
としてお
かなければなりません。ここで という太字はその量がベクトルである、という意味です。 またそもそ
も加速度とは速度の微分、そして速度は物体の位置
という太字はその量がベクトルである、という意味です。 またそもそ
も加速度とは速度の微分、そして速度は物体の位置 の微分でしたね。よってニュートンの運動方程式
は
の微分でしたね。よってニュートンの運動方程式
は
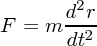 | (2.1) |
と書き改められます。さて、これの何が変わったんだといわれると、一番は力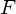 と物体の位置
と物体の位置 の方程式になっていま
す。つまり力が分かれば物体の位置がわかるわけです。ただし問題は物体の位置
の方程式になっていま
す。つまり力が分かれば物体の位置がわかるわけです。ただし問題は物体の位置 が二回微分になっていることです。こ
のような微分のある式を微分方程式と呼びます。この微分方程式を具体的にどう解くのかひとつ例を出しま
す。
が二回微分になっていることです。こ
のような微分のある式を微分方程式と呼びます。この微分方程式を具体的にどう解くのかひとつ例を出しま
す。
2.1 地上付近での重力下の運動
地上付近での重力は一様で鉛直下方向に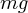 です。 m は質量、 g は重力定数です。さて、鉛直上方向を y 軸の向きとする
と運動方程式は
です。 m は質量、 g は重力定数です。さて、鉛直上方向を y 軸の向きとする
と運動方程式は
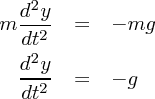
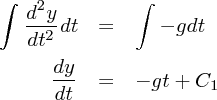
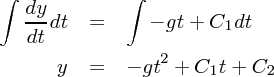
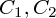 てのが突然出てきましたがこれはいわゆる積分定数です。二回微分なので運動方程式を解
くと必ずこの積分定数が二つ出てきます。この積分定数はどうやって決まるの?という疑問が当然浮かぶと思いますが、そ
れは最初の状態がどうなっているのか、初期条件によって決まります。初期条件というのはある時間の物体の位置と速度と
いうのが一般的です。つまり最初にどこからどのくらいの速さで投げるのかといった情報です。たとえば今の場合、
てのが突然出てきましたがこれはいわゆる積分定数です。二回微分なので運動方程式を解
くと必ずこの積分定数が二つ出てきます。この積分定数はどうやって決まるの?という疑問が当然浮かぶと思いますが、そ
れは最初の状態がどうなっているのか、初期条件によって決まります。初期条件というのはある時間の物体の位置と速度と
いうのが一般的です。つまり最初にどこからどのくらいの速さで投げるのかといった情報です。たとえば今の場合、
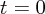 で
で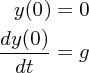
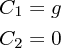
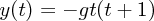
という放物線軌道が得られます。
2.2 単振動
こんな調子でばねによる単振動を今度は解いてみましょう。ばねの力はばね係数 k とばねの自然長からの変位 x の積
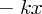 で表されますので運動方程式は
で表されますので運動方程式は
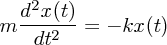
となります。さてこれを解くのにまた積分しようかといきたいところですが求めるべき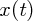 が右辺にも入っていてなんだ
かにっちもさっちもいきません。じゃあ、どうしようかいうと当てずっぽうで
が右辺にも入っていてなんだ
かにっちもさっちもいきません。じゃあ、どうしようかいうと当てずっぽうで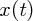 の形を予測していきます。実は微
分方程式を解く方法で最も有力な方法が当てずっぽうです。なんて頼りないんだと感じるでしょうが事実
なので仕方ありません。二次方程式のように絶対的な公式なんかはありません。それゆえ、微分方程式は
解けない(解けていない)もののほうが多いんです。解ける微分方程式は特殊なものいってもいいでしょ
う。
の形を予測していきます。実は微
分方程式を解く方法で最も有力な方法が当てずっぽうです。なんて頼りないんだと感じるでしょうが事実
なので仕方ありません。二次方程式のように絶対的な公式なんかはありません。それゆえ、微分方程式は
解けない(解けていない)もののほうが多いんです。解ける微分方程式は特殊なものいってもいいでしょ
う。
さて、今回の場合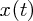 の二回微分が
の二回微分が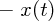 になるようなもの。それは実は三角関数
になるようなもの。それは実は三角関数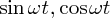 です。ためしに
突っ込んでみましょう。
です。ためしに
突っ込んでみましょう。
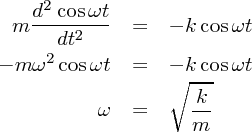
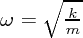 とすればちゃんと満たしていることがわかりますね。
とすればちゃんと満たしていることがわかりますね。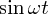 も同様に満たします。ただ、これを定数倍した
もの
も同様に満たします。ただ、これを定数倍した
もの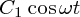 もまたその足し合わせ
もまたその足し合わせ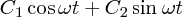 も運動方程式を満たします。そう、実はこの定数が二つある
最後の形が一般の解なのです。この式を
も運動方程式を満たします。そう、実はこの定数が二つある
最後の形が一般の解なのです。この式を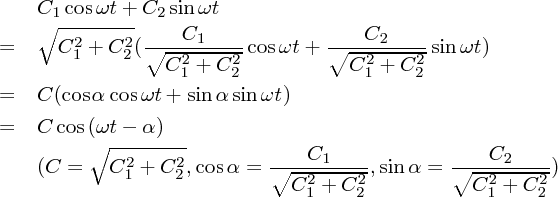
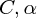 については初期条件によります。
については初期条件によります。
