Chapter 1
ニュートン力学の三つの公理
1.1 ニュートンの運動方程式
「力学」とは力について考える学問です。さてその力とはなんでしょう?その疑問の答えのためにちょっと歴史を追ってみ ましょう。
「力学」の歴史はまず、ガリレイの等速直線運動の原理(「慣性の法則」)から起こります。これは「物体は何もされ なければ等速で真っ直ぐに動き続ける」というものです。(実はちょっと違うのですがあとで述べます)普段の感 覚からいくと動かすことにこそなにか力が要りそうですが、勝手に物が止まってしまうのも地面なんかと こすれてしまうからなんです。つまり、物体に「何かして等速から変化させるもの」こそが「力」なわけ です。さてその力 F が大きければ大きいほど速度が変化するわけなんで、速度の変化分=加速度 a を使っ て
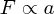
と書けることにしましょう。さて比例関係なんで適当な比例係数 m をとってやれば
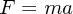 | (1.1) |
とかけます。どっかで見たことある式になったかと思いますが、これがニュートンの運動方程式です。自然 な形ではありますがつまりこれは力を定義する式だったわけです。それゆえ公理のひとつなわけです。さ て、今比例係数 m は適当にとったものであり、質量でも何でもありません。が実はこれが物の重さ(重力質 量)と一致するので(あとで述べます) m が質量になり完全に教科書に載っている形になったかと思いま す。
1.2 慣性の法則
先ほど「慣性の法則」=「物体は何もされなければ等速で真っ直ぐに動き続ける」といいましたが、それなら運動方程 式
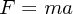
から F=0 とすれば a=0、つまり等速直線運動で運動方程式から示せるのでわざわざ公理のうちにいれなくても運動方程式 だけで十分になってしまいます。実は慣性の法則にはもうひとつ、そしてそちらのほうがより重要なものがあるので す。
それは「あらゆる慣性系で物理法則は変わらない」というものです。慣性系というのは等速直線運動してい るものの集団のようなものです。例えば新幹線の車内とか地球上(厳密には地球は円運動なんで違うので すが半径が大きいので近似的に等速直線運動とします)だとかです。もし慣性系によって物理法則が違っ たなら、火星と地球で別々の物理を作らなきゃいけなくなったりしていまったり、また地球上、あるいは 太陽系で実験している限り永遠に宇宙全体の法則を理解できないということになり、我々が地球人である 以上やむをえない最低限の仮定であり、また宇宙でそんなご当地ルールがあるのはなんだか不自然ですよ ね。
そんなわけでこの「慣性の法則:あらゆる慣性系で物理法則は変わらない」という公理は実はニュートン力学に留まら ず相対論・量子力学にいたる物理全体の重要な公理であり現在実験的にもこれを破る事実は見つかっていませ ん。
1.3 作用・反作用の法則
三番目最後の公理に作用・反作用の法則があります。これは「力は同時に同じ大きさで反対向きのものと対になって働く」 というものです。
例えば真っ暗な宇宙空間で物体 A が物体 B とぶつかって離れるという現象があったとき、
- A から見ると、自分は止まっていて B が近づいてきてぶつかったので B から力を加えられて A が飛ばされ たように見えます。
- B からは A が飛んできて、ぶつかったので A から力を加えられて自分が飛ばされたように見えるでしょ う。
- 離れたところから見ていた C からは A と B が共に近づいて、そしてお互いに力をかけ合ってまた離れたよ うに見えるでしょう。
さて結局どちらがどっちに力を加えたのでしょうか?慣性の法則より等速直線運動である限り A,B,C どれから見たもの とも矛盾しない形にしなくてはいけません。とすると
- A は B から力を受けた(A から見たとき)
- B は A から力を受けた(B から見たとき)
- A と B ともに力を受けた(C から見たとき)
から矛盾のないのは「力は A と B 同時に同じ大きさで反対向きのものが対になって働いたとき」なわけです。
さて公理が三つそろったところで、次に具体的な問題についていろいろ求めてみましょう。
