Chapter 2
積分
積分は微分の逆演算で
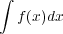 | (2.1) |
と表記し
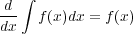 | (2.2) |
または
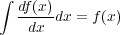 | (2.3) |
という関係で定義される。
2.1 積分の例
xの累乗
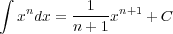
三角関数
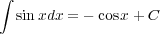
証明は右辺を微分すれば明らか。 C は積分定数と呼ばれ、この定数は何でも構わない(微分すれば消えるので)積分には常 にこの不定性が付きまとう。
2.2 定積分
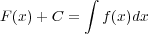
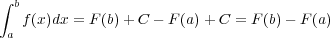
を定積分といい、 f(x) の x=a から b までの面積に相当する。
2.3 積分の直感的理解と面積
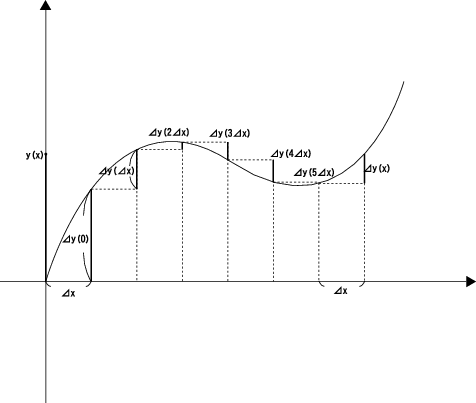
微分の直感的な概念が
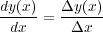
だったので、これを元のyに戻す操作こそが積分のはずで
まず、
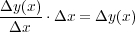
とすると、 x での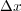 だけ x が変化したときの y の変化
だけ x が変化したときの y の変化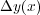 が得られるが、これだけでは y(x) には程遠い。 y(x) を
得るためには x が 0 〜 x までの
が得られるが、これだけでは y(x) には程遠い。 y(x) を
得るためには x が 0 〜 x までの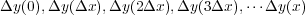 を全て足し合わせてやればいいはず
で
を全て足し合わせてやればいいはず
で
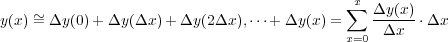
一番右辺の項で
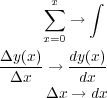
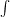 は Sum(足し上げる) の S を文字ったものからきてます。ただ、この際
x=0 での y の値 y(0) の情報は微分からは得られないので、この部分の不定性が積分定数 C の不定性となって出てくると解
釈できます。
は Sum(足し上げる) の S を文字ったものからきてます。ただ、この際
x=0 での y の値 y(0) の情報は微分からは得られないので、この部分の不定性が積分定数 C の不定性となって出てくると解
釈できます。
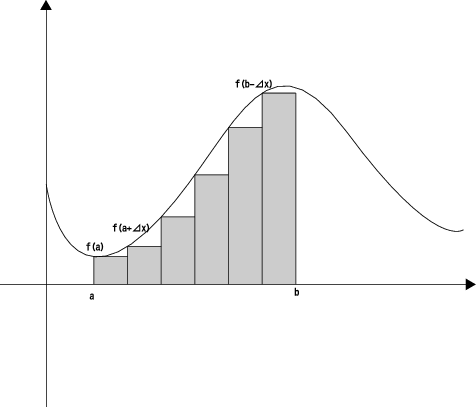
この考えで
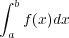
という定積分を見てみると
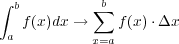
でこれは f(a) から f(b) までの面積と確かに考えられます。
2.4 積分の性質
2.4.1 積分変数の変換
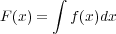
に対して積の微分の公式を使い
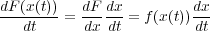
両辺tで積分すると
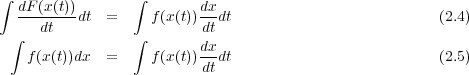
2.4.2 部分積分
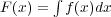 ならば
ならば
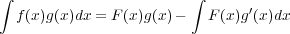 | (2.6) |
という関係がある。これを部分積分という。
証明は積の微分の公式を使い
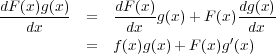
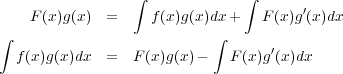
積分変数の変換や部分積分は積分計算で非常によく使うテクニックです。