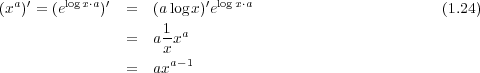Chapter 1
微分
1.1 微分の定義
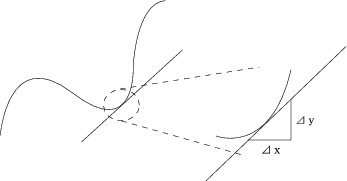
微分とは接線の傾きと解釈できるもので、感覚的には
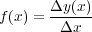
です。
厳密には、極限(h を0に限りなく近づける)を使って
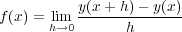 | (1.1) |
微分の記号は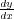 や
や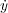 や
や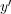 という風に書きます。
という風に書きます。
1.1.1 例 累乗の微分
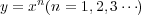 を微分すると
を微分すると
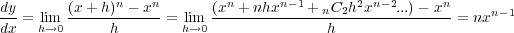 | (1.2) |
となる
1.2 微分の公式
1.2.1 積の公式
二つの関数の積の微分は以下のようになる
![′ 1-
(f(x)g(x)) = lim h (f(x+ h)g(x+ h)- f(x)g(x)) (1.3)
1-
= lim h (f(x+ h)g(x+ h)- f(x)g(x)- f(x)g(x + h)+ f(x)g(x + h))
1-
= lim h [(f (x + h)- f(x))g(x +h )+ f(x)(g(x+ h)- g(x))]
= f′(x)g(x) +f (x)g′(x)](math8x.png)
1.2.2 合成関数
関数の中に関数が入れ子になっているような合成関数の微分は以下のようになる
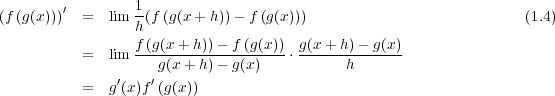
この二つの公式は大変よく使う。
1.3 三角関数と微分
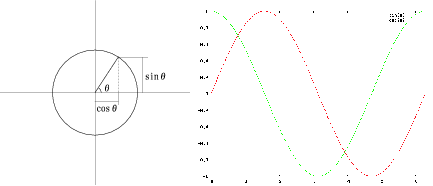
三角関数の幾何学的な定義は、半径1の円の弧 のときの縦の長さが
のときの縦の長さが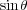 、横の長さが
、横の長さが 。角度はラジアンを使っ
ています(180° = π、 360° =2 π)
。角度はラジアンを使っ
ています(180° = π、 360° =2 π)
1.3.1 加法定理
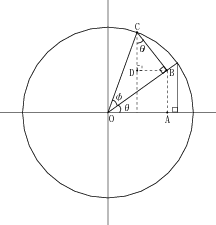
角度の和をとった三角関数には以下のような公式がある。二つの角の和が0からπ /2 までのときは図1.3を参照してくださ い。(それ以降の角のときの証明は省略します)
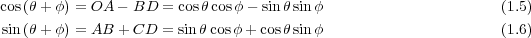
1.3.2 角度が小さいときの近似
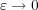 で接線の傾きは横軸に直角なことから
で接線の傾きは横軸に直角なことから

1.3.3 三角関数の微分
微分は加法定理と角度が小さいときの近似を使えば
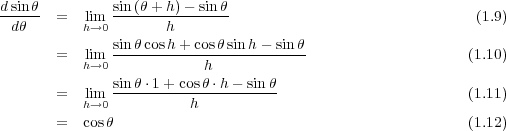
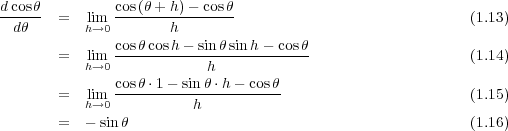
1.4 指数関数の微分とネイピア数
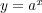 という指数関数を微分しようとした場合
という指数関数を微分しようとした場合
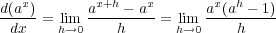
となりこれ以上計算できないが で
で
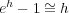
となるような数のとき
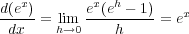
で計算できる
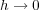 で
で

このような e という数がちゃんと有限の値になるのか疑問なので
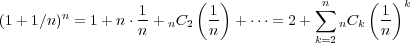
と展開してみるとわかるが eソ2 がわかる。さらに
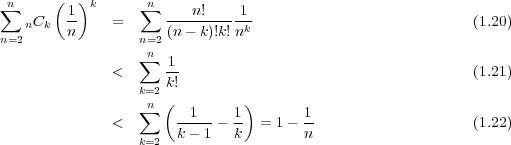
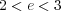
と示せる。実際数値計算により
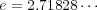
となることが知られている。この e を使えば一般の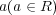 に対しても
に対しても
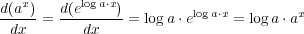
と計算できる。
1.5 その他の関数
1.5.1 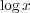 の微分
の微分

1.5.2 一般の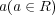 の累乗の微分
の累乗の微分